线性变换与矩阵乘法
在前面的章节中,我们指出矩阵
线性变换的定义
设
和 是两个线性空间,如果存在一个映射 ,使得对于任意的 和任意的常数 ,都有
可加性:
齐次性:
那么我们称映射
是一个线性映射。
如果,一个线性映射是从一个线性空间到它自身的映射,即
对于一组基
可以验证,变换
- 如果
,那么 - 可加性:
- 齐次性:
二维线性变换
在这一小节,我们尝试以二维线性变换为例,从几何的角度来感受一下线性变换。根据上文的定义,我们知道一个二维的线性变换可以用一个
这个矩阵可以将一个二维向量
于此同时,我们对于二维平面上的一些常见操作,比如旋转,缩放等等,都比较熟悉,那么这些操作如何用矩阵来表示呢?
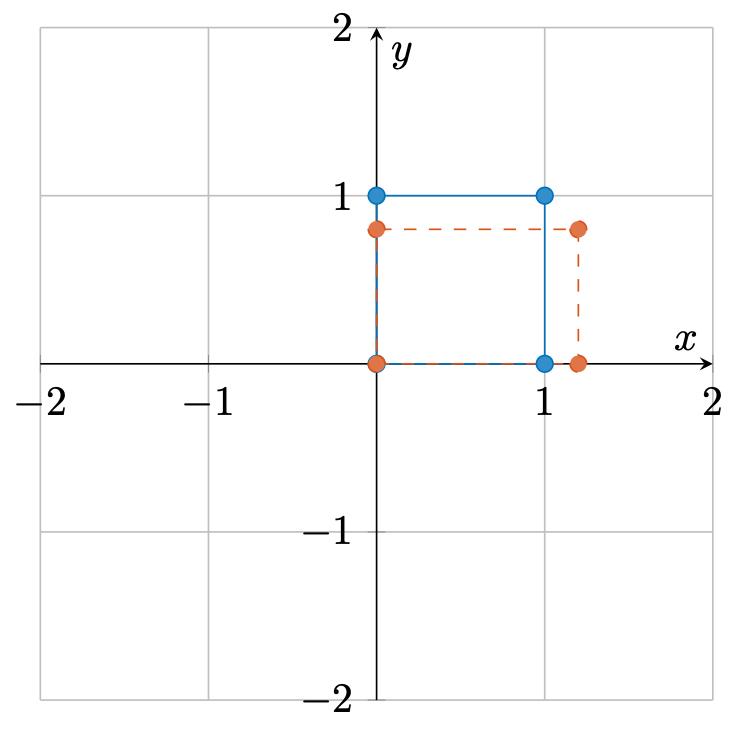
缩放
可以发现,变换后的向量分别在两个方向上被缩放了
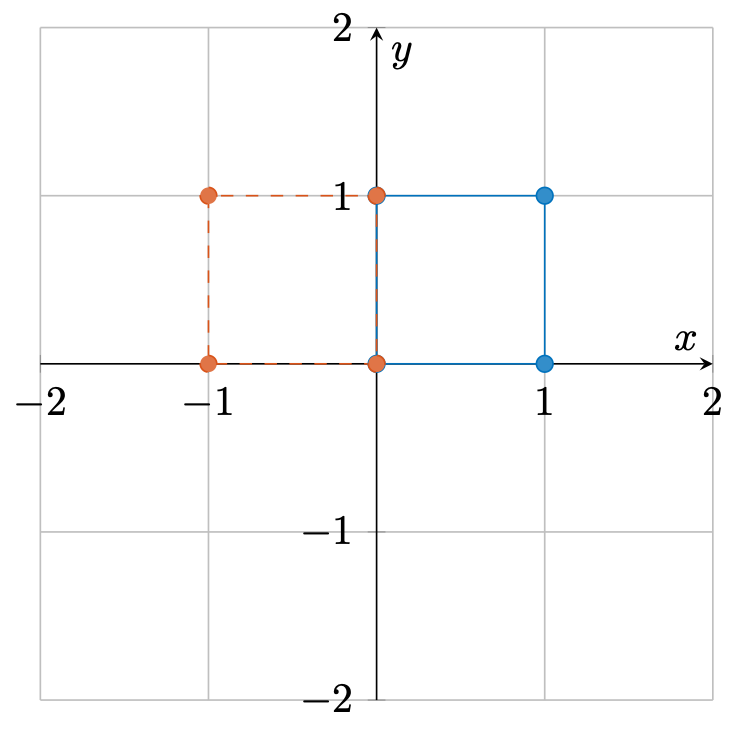
倍 反射
此时,变换后的向量在第一个轴上被反转了
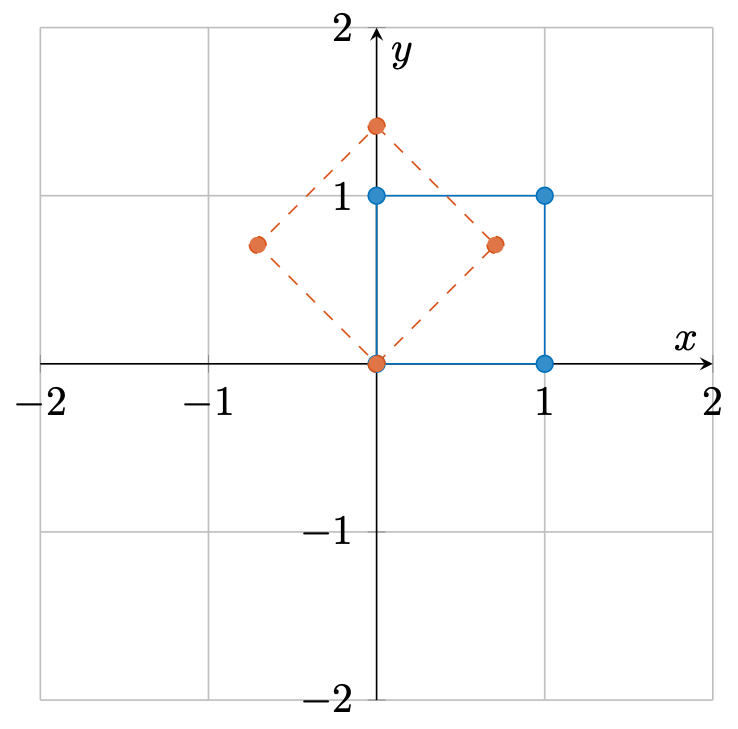
旋转
该矩阵相当将向量以原点为中心旋转了
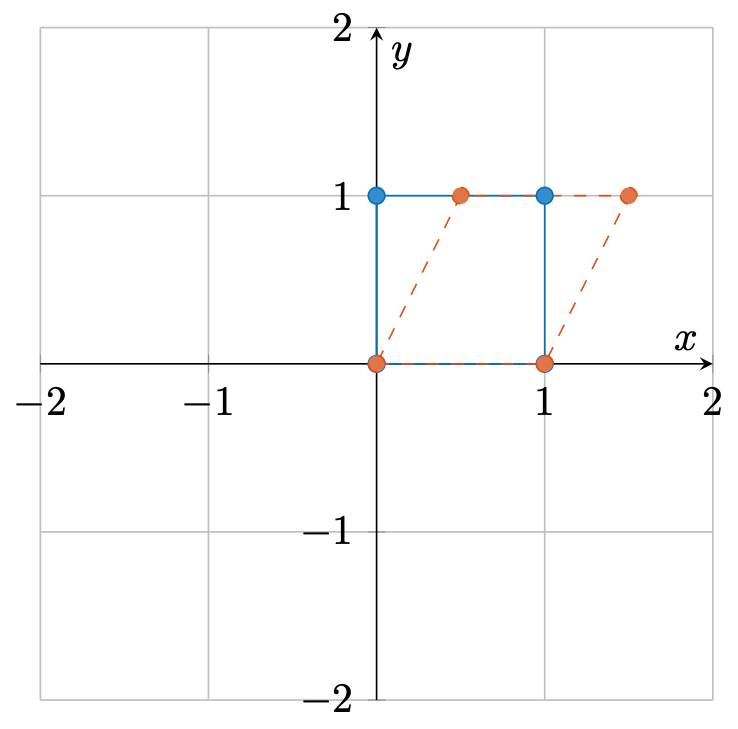
度 剪切
此时,变换后的向量为
线性变换的组合
两个乃至多个线性变换的组合依旧是一个线性变换吗?这里我们简单证明一下,设有两个线性变换
即线性变换的组合构成的新的变换
- 如果
,那么 - 可加性:
- 齐次性:
因此,
注意到,对于线性变换
令
设
变换后向量的第
对比式 (1) 和式 (2) 可知,变换矩阵
为了表达美观,我们可以将对应的变量进行替换,得到如下表达式
我们将式 (3) 中的运算称作矩阵乘法,记作
实际上,矩阵乘法可以这样计算,如
此外,上文的推导都是基于方阵的(也就是行和列具有相同长度的矩阵)。对于一般的矩阵,同样可以使用矩阵乘法来计算,设有矩阵
可以看到,如果两个矩阵能够进行矩阵乘法,那么第一个矩阵的每一行都和第二个矩阵的每一列都有相同的长度。正是这样,矩阵乘法并不满足交换率,显然
小结
- 线性变换可以用矩阵表示
- 常见的线性变换就几何意义来说,有缩放、反射、旋转、剪切
- 线性变换的组合可以用矩阵乘法表示