向量的基本运算

向量是向量空间中的一个元素，除了最基本的加法和数乘运算外，还有一些其他的运算。当然，正如向量空间有着明确的几何意义一样（比如二维向量空间是一个平面），这些运算我们同样也可以从几何的角度来理解。

当然，在介绍这些运算之前，我们先来回顾一下向量最基本的加法和数乘运算。设向量 $\mathit{x},\mathit{y}$ 都为 $n$ 维向量空间 $V$ 中的元素，那么向量的加法运算定义为：

$$\mathit{x}+\mathit{y}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]+\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]=\left[\begin{array}{c}{x}_1+y_1\\ x_2+y_2\\ ⋮\\ x_n+y_n\end{array}\right]$$

设 $\alpha$ 为实数，那么向量的数乘运算定义为：

$$\alpha \mathit{x}=\alpha \left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}\alpha x_1\\ \alpha x_2\\ ⋮\\ \alpha x_n\end{array}\right]$$

向量的内积

内积是向量空间中最基本的运算之一，它不仅可以用来定义向量的长度，还可以用来定义向量之间的夹角。我们首先给出内积的定义。

给定两个 $n$ 维向量 $\mathit{x},\mathit{y}$，它们的内积定义为：

$$⟨\mathit{x},\mathit{y}⟩=x_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n=\sum _{i=1}^n{x}_i{y}_i.$$

简单来说，就是将两个向量对应位置的元素相乘，然后再将所有的乘积相加。并且，我们可以发现，内积满足如下性质：

$$⟨\mathit{x},\mathit{y}+\mathit{z}⟩=⟨\mathit{x},\mathit{y}⟩+⟨\mathit{x},\mathit{z}⟩.$$

那么，在给定内积的定义后，我们就可以进一步地给出向量的模长的计算公式：

$$\parallel x{\parallel }^2=⟨\mathit{x},\mathit{x}⟩=x_1^2+x_2^2+\cdots +x_n^2.$$

换句话说就是，一个向量的模长的平方等于这个向量与自身的内积。

接下来，我们需要回忆一下三角形余弦公式：

$$\parallel \mathit{c}{\parallel }^2=\parallel \mathit{a}-\mathit{b}{\parallel }^2=\parallel \mathit{a}{\parallel }^2+\parallel \mathit{b}{\parallel }^2-2\parallel \mathit{a}\parallel \parallel \mathit{b}\parallel \cos \theta ,$$

其中 $\mathit{a},\mathit{b},\mathit{c}$ 为三角形三个边，而$\theta$ 为 $\mathit{a}$ 与 $\mathit{b}$ 的夹角。

与此同时，根据模长的计算公式，我们有

$$\begin{array}{rl}\parallel \mathit{a}-\mathit{b}{\parallel }^2& =⟨\mathit{a}-\mathit{b},\mathit{a}-\mathit{b}⟩\\ & =⟨\mathit{a},\mathit{a}⟩+⟨\mathit{b},\mathit{b}⟩-2⟨\mathit{a},\mathit{b}⟩\\ & =\parallel \mathit{a}{\parallel }^2+\parallel \mathit{b}{\parallel }^2-2⟨\mathit{a},\mathit{b}⟩.\end{array}$$

对比上面两个公式，我们可以发现，两个向量之间的内积与它们的模长以及夹角之间存在着如下关系：

$$⟨\mathit{a},\mathit{b}⟩=\parallel \mathit{a}\parallel \parallel \mathit{b}\parallel \cos \theta .$$

因此，两个向量之间的夹角可以通过如下公式计算：

$$\cos \theta =\frac{⟨\mathit{a},\mathit{b}⟩}{\parallel \mathit{a}\parallel \parallel \mathit{b}\parallel }.$$

如此一来，向量的内积的几何意义就非常清晰了。不妨令向量 $\mathit{b}$ 的模长为 1，那么向量 $\mathit{a}$ 在向量 $\mathit{b}$ 上的投影长度就是 $\parallel \mathit{a}\parallel \cos \theta$，而这就刚好等于 $⟨\mathit{a},\mathit{b}⟩$。

图1. 向量内积

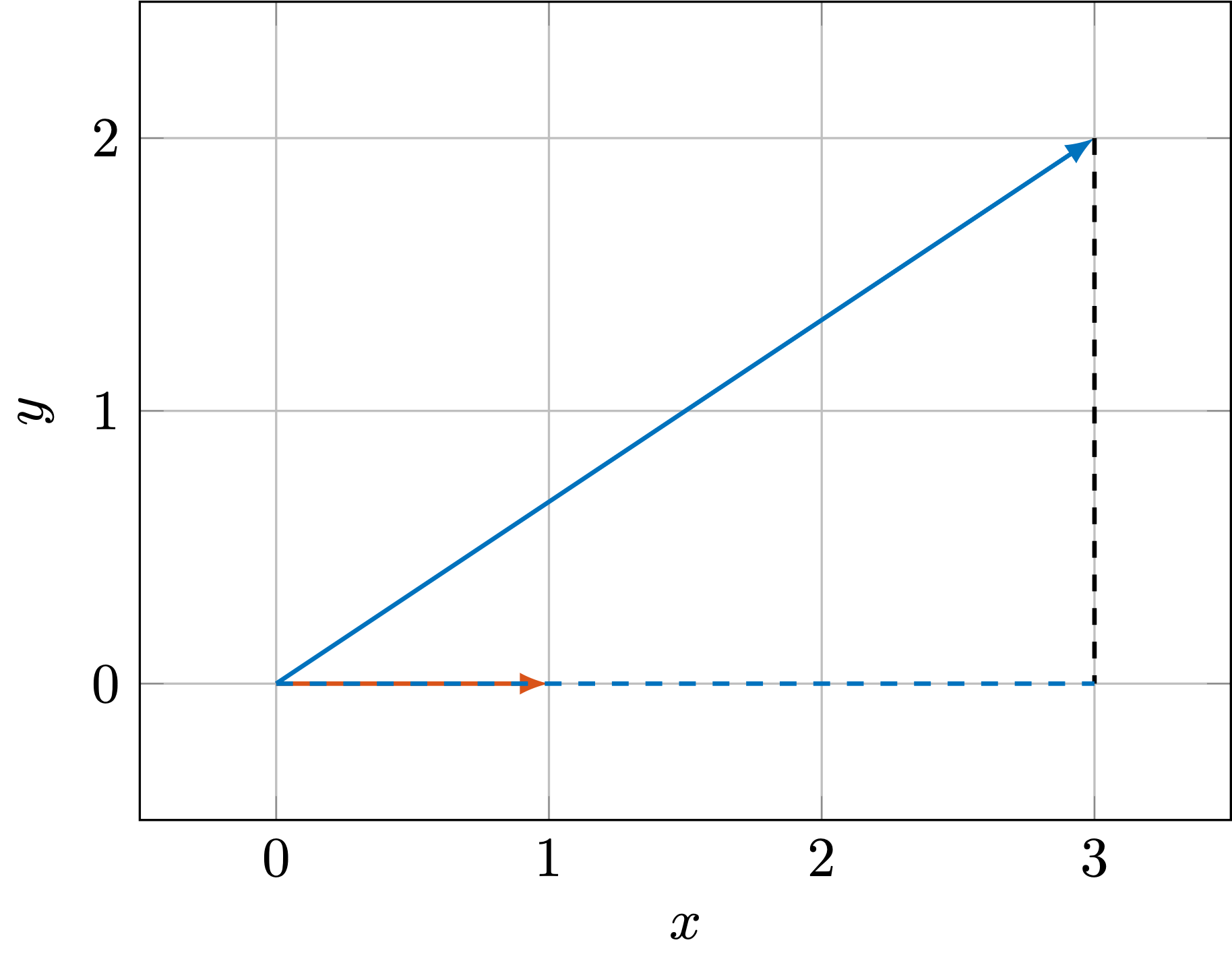
向量的线性组合

由于线性空间是加法和数乘封闭的，因此我们自然很关心多个向量以及他们的组合之间有什么联系。首先，我们先给出向量的线性组合的定义：

给定 $m$ 个 $n$ 维向量，${\mathit{x}}_1,{\mathit{x}}_2,\cdots ,{\mathit{x}}_k\in {\mathbb{R}}^{n\times 1}$，以及一个 $m$ 维列向量 $\mathit{v}={\left[\begin{array}{cccc}{v}_1& v_2& \cdots & v_m\end{array}\right]}^{\mathrm{T}}$，那么这 $m$ 个向量的线性组合定义为：

$$\mathit{y}=v_1{\mathit{x}}_1+v_2{\mathit{x}}_2+\cdots +v_k{\mathit{x}}_m.$$

如果我们将这 $m$ 个向量写成如下的形式：

$$\begin{array}{rl}\mathbf{X}& =\left[\begin{array}{cccc}{\mathit{x}}_1& {\mathit{x}}_2& \cdots & {\mathit{x}}_m\end{array}\right],\\ & =\left[\begin{array}{cccc}{X}_{11}& X_{12}& \cdots & X_{1m}\\ X_{21}& X_{22}& \cdots & X_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ X_{n1}& X_{n2}& \cdots & X_{nm}\end{array}\right],\end{array}$$

显然，$X_{ij}$ 为向量 ${\mathit{x}}_j$ 的第 $i$ 个元素，并且 $\mathbf{X}$ 是一个有着 $n\times m$ 元素的阵列，被称作矩阵。通常情况下，我们使用加粗的大写正体字母来表示矩阵，用如下的形式来标明矩阵的大小：

$$\mathbf{X}\in {\mathbb{R}}^{n\times k}.$$

与此同时，矩阵与向量的乘法被定义为：

给定一个 $n\times m$ 的矩阵 $\mathbf{X}$，以及一个 $m$ 维向量 $\mathit{v}$，那么矩阵与向量的乘法定义为：

$$y_i=(\mathbf{X}\mathit{v}{)}_i=\sum _{j=1}^m{X}_{ij}{v}_j.$$

其中 $y_i$ 为向量 $\mathit{y}$ 的第 $i$ 个元素，$(\mathbf{X}\mathit{v}{)}_i$ 则表示矩阵乘以向量的结果的第 $i$ 个元素。通常情况下，我们将矩阵与向量的乘法写成如下的形式：

$$\mathit{y}=\mathbf{X}\mathit{v}.$$

尽管矩阵与向量的乘法看起来有些复杂，但是我们可以发现，矩阵与向量的乘法等价于向量的线性组合：一个矩阵 $\mathbf{X}\in {\mathbb{R}}^{n\times m}$ 乘以一个向量 $\mathit{v}\in {\mathbb{R}}^{m\times 1}$，实际上就是对矩阵的每一列进行线性组合，而向量 $\mathit{v}$ 中的每一个元素则是对应的线性组合的系数，即

$$\mathit{y}=\mathbf{X}\mathit{v}=\left[\begin{array}{cccc}{\mathit{x}}_1& {\mathit{x}}_2& \cdots & {\mathit{x}}_m\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_m\end{array}\right]=v_1{\mathit{x}}_1+v_2{\mathit{x}}_2+\cdots +v_k{\mathit{x}}_m.$$

特别地，当 $\mathbf{X}={\mathit{x}}^{\mathrm{T}}=\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_m\end{array}\right]\in {\mathbb{R}}^{1\times m}$ 时，也就是矩阵 $\mathbf{X}$ 实际上是一个行向量时，此时矩阵与向量的乘法就是向量的内积：

$$y=\mathbf{X}\mathit{v}=\sum _{i=1}^m{x}_i{v}_i=⟨\mathit{x},\mathit{v}⟩.$$

因此当给定两个维度相同的列向量$x,y\in {\mathbb{R}}^{n\times 1}$时，我们可以将它们的内积写成如下的形式：

$$⟨\mathit{x},\mathit{y}⟩={\mathit{x}}^{\mathrm{T}}\mathit{y}.$$

从几何的角度来说，向量的线性组合就是将一组向量拉伸或者压缩，然后再将它们相加。比如，图 2 中的两个向量

$${\mathit{x}}_1=\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right],{\mathit{x}}_2=\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right].$$

图2. 线性组合的几何示意

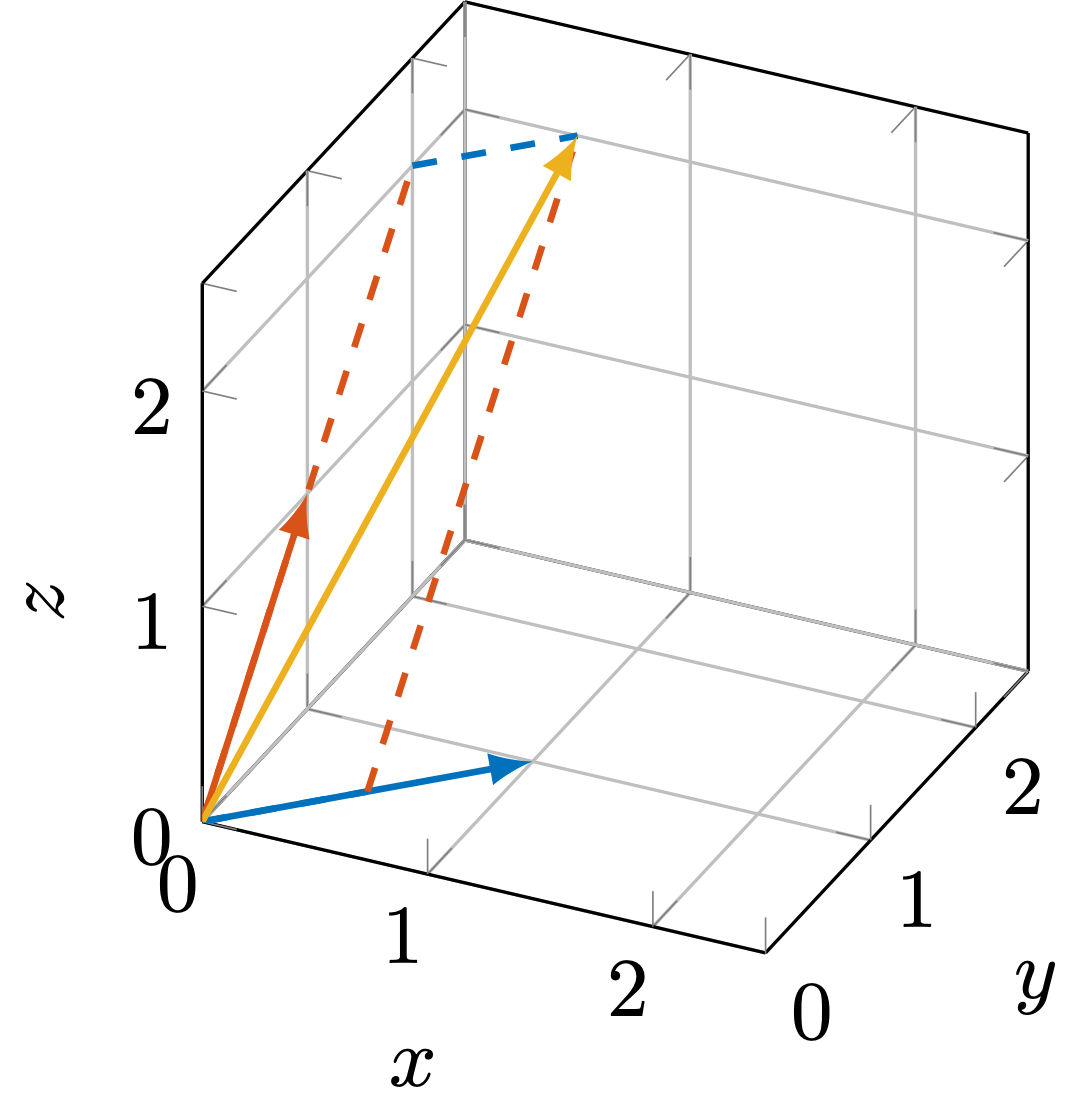
用组合系数 $\mathit{v}={\left[\begin{array}{cc}0.5& 2\end{array}\right]}^{\mathrm{T}}$来对这两个向量进行线性组合，我们可以得到如下的结果：

$$\mathit{y}=0.5\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]+2\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}0.5\\ 2.5\\ 2\end{array}\right].$$

也就是图 2 中的黄色箭头所指示的向量。

小结

本节介绍了向量的内积以及向量的线性组合。向量的内积可以用来定义向量的模长以及向量之间的夹角，而向量的线性组合则引出了矩阵与向量的乘法。此外，对于这两种运算，我们还从几何的角度来理解了它们的意义。