关于两次反射为旋转的思考

在二维平面上，对一个物体进行两次反射操作为什么等价于一个旋转操作呢？我们当然可以从最简单的几何出发，用小学生都知道的知识来证明这个结论。然而正如数学家 Arnold Ross 所说：“The purpose of proof is to understand, not to verify.”, 用更抽象的数学工具来证明这个结论，可以得到更深刻的理解。在本文中，通过使用群这一工具来推导该一结论，我们可以发现该几何性质的成立源自于旋转操作和反射操作构成的群的结构。

推导

令 $R_{\theta }$ 为沿着逆时针旋转 $\theta$ 度；而 $F_{\theta }$ 为沿着角度为 $\theta$ 的对称轴进行反射；如下图所示。

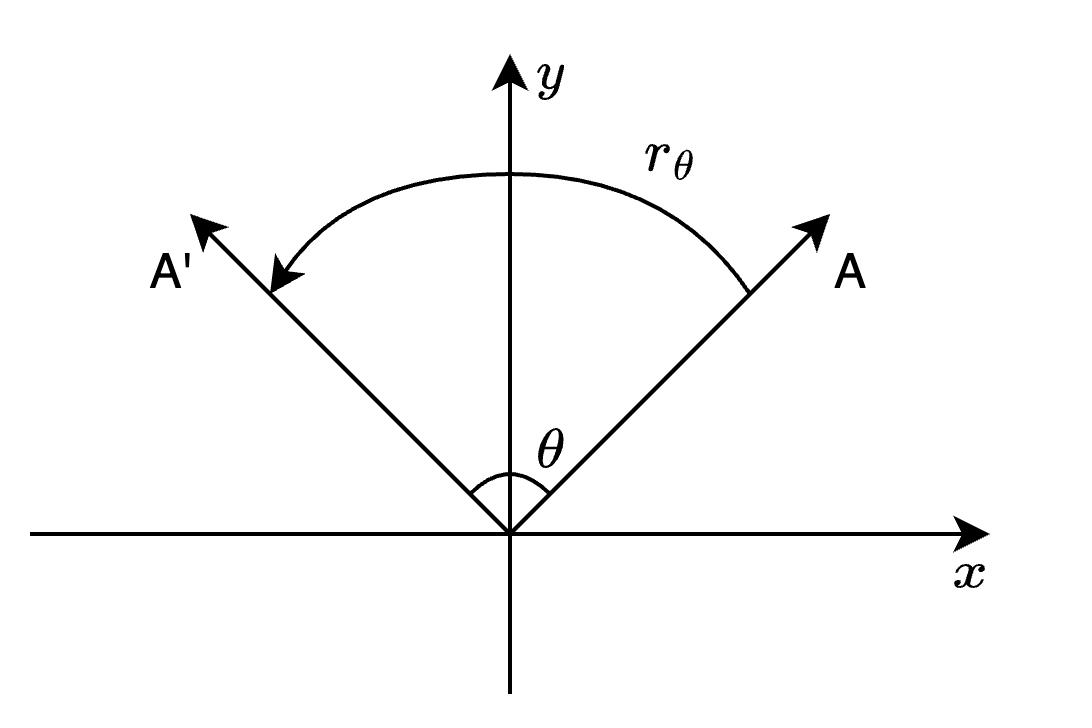
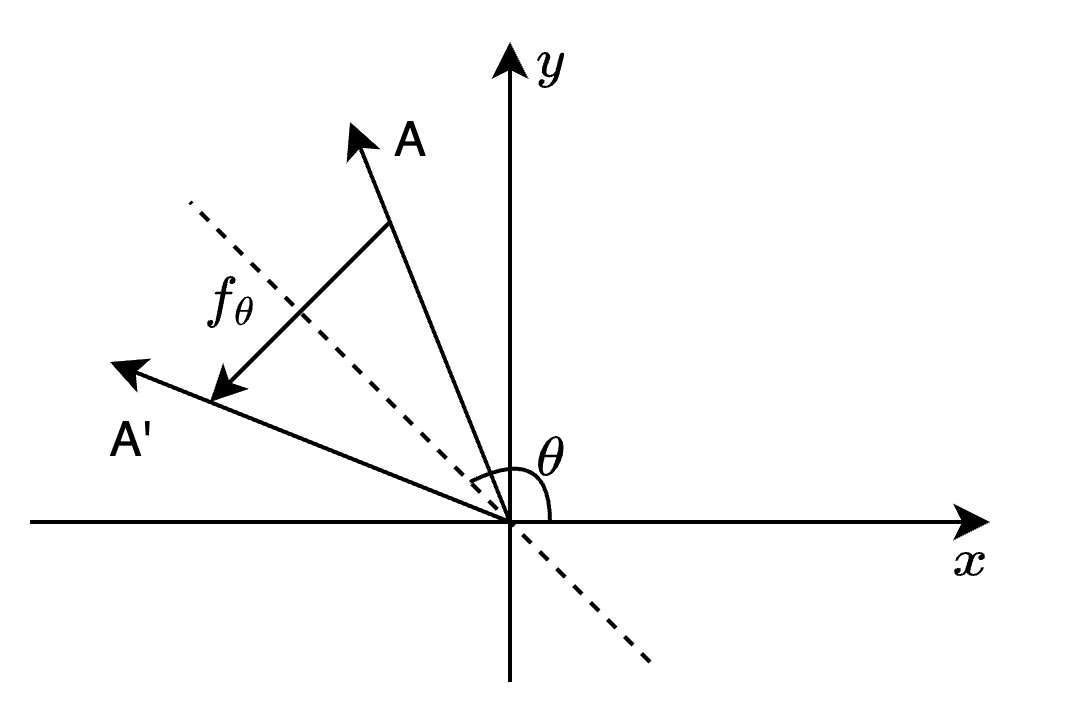
图1. 旋转和反射操作

不难发现，对于一个与 $x$ 轴夹脚为 $\alpha$ 的向量，经过 $R_{\theta }$ 的作用后与 $x$ 轴夹角为：

$$R_{\theta }(\alpha )=\alpha +\theta .$$

与此同时，经过 $F_{\theta }$ 的作用后与 $x$ 轴夹角为：

$$F_{\theta }(\alpha )=2\theta -\alpha .$$

基于这两个等式，我们可以得到：

$$\begin{array}{rl}(F_{{\theta }_2}\circ F_{{\theta }_1})(\alpha )=& F_{{\theta }_2}(F_{{\theta }_1}(\alpha ))=F_{{\theta }_2}(2{\theta }_1-\alpha )\\ =& 2{\theta }_2-(2{\theta }_1-\alpha )=\alpha +2({\theta }_2-{\theta }_1)\\ =& R_{2{\theta }_2-2{\theta }_1}.\end{array}$$

因此两次反射操作等价于一个旋转操作，即

$$F_{{\theta }_2}\circ F_{{\theta }_1}=R_{2{\theta }_2-2{\theta }_1}.$$

事实上，前面的几何推导的成立是由旋转和缩放操作构成的群的结构决定的。不妨假设有这样一个集合

$$G=R\cup F$$

其中，$R=\{R_{\theta }\}$ 为所有可能的旋转构成的集合， $F=\{F_{\theta }\}$ 为所有可能的反射构成的集合。注意到，$R\cap F=\varnothing$ ，也就是说不可能有某一个操作既是旋转也是反射。

不难验证 $G$ 构成了一个群，简单来说，这个集合是对圆的对称性的描述，一个圆旋转任意角度还是相同的圆，一个圆沿任意角度反射还是相同的圆，如下图所示。

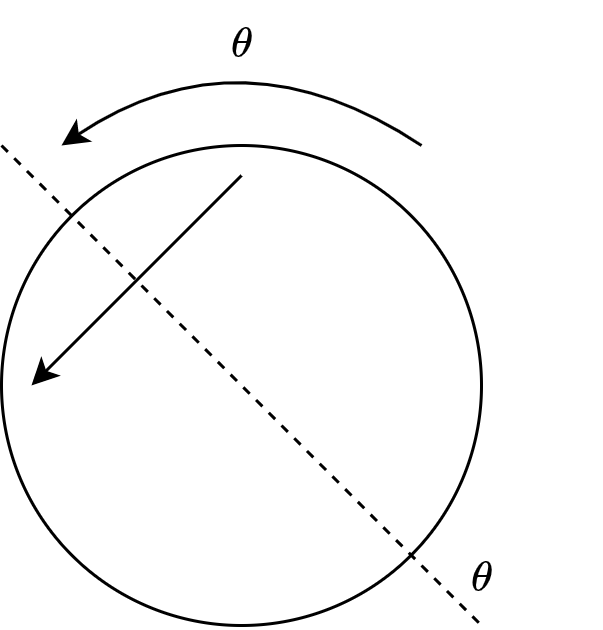
进一步地，可以发现 $R$ 是 $G$ 的一个子群（任意两个旋转的组合还是一个旋转）。由于 $F_{\theta }\notin R$，所以 $R$ 在 $G$ 中对应的左右陪集有如下性质：

$$F_{\theta }R\cap R=R{F}_{\theta }\cap R=\varnothing$$

这表明 $F_{\theta }R\subseteq F,R{F}_{\theta }\subseteq F$，也就是说任意一个旋转和反射的组合（无论顺序如何）都是一个反射。下面我们假设在所有的反射中存在两个反射，它们的组合为一个反射：

$$F_{{\theta }_1}\circ F_{{\theta }_2}\in F$$

我们可以验证，只要存在一对这样的反射，那么任意两个反射的组合都为一个反射：

因为 $F_{{\theta }_1}\circ F_{{\theta }_2}\in F,R_{{\varphi }_1}\in R,R_{{\varphi }_2}\in R$，所以

$$\begin{array}{rl}& (F_{{\theta }_1}\circ R_{{\varphi }_1})\circ (R_{-{\varphi }_1}\circ F_{{\theta }_2}\circ R_{{\varphi }_2})\\ =& F_{{\theta }_1}\circ (R_{{\varphi }_1}\circ R_{-{\varphi }_1})\circ F_{{\theta }_2}\circ R_{{\varphi }_2}\\ =& F_{{\theta }_1}\circ F_{{\theta }_2}\circ R_{{\varphi }_2}\in F\end{array}$$

令 $F_{{\theta }_1^{\prime }}=F_{{\theta }_1}\circ R_{{\varphi }_1}$，$F_{{\theta }_2^{\prime }}=R_{-{\varphi }_1}\circ F_{{\theta }_2}\circ R_{{\varphi }_2}$，注意到 $F_{{\theta }_1^{\prime }}$ 和 $F_{{\theta }_2^{\prime }}$ 的选取是任意且无关的。因此，对于任意的 ${\theta }_1^{\prime }$ 和 ${\theta }_2^{\prime }$，我们都有

$$F_{{\theta }_1^{\prime }}\circ F_{{\theta }_2^{\prime }}\in F$$

由于一个反射操作与自身的组合为单位操作 $R_0$，即旋转 $0$ 度，所以

$$F_{\theta }\circ F_{\theta }=R_0\in R$$

而这与 $F_{{\theta }_1^{\prime }}\circ F_{{\theta }_2^{\prime }}\in F$ 相悖，所以任意两个反射操作的结合一定为旋转操作。

不仅如此，在离散情况下，我们还有一个很有意思的证明方法：对于一个正 $n$ 边形，对应的二面体群 $D_n$，包含了 $n$ 个旋转操作和 $n$ 个反射操作。如果任意两个反射操作的结合仍为一个反射操作，那么有这 $n$ 个反射操作再加上单位操作（一共是 $n+1$ 个）构成了 $D_n$ 的一个子群。

而一个有限群的子群的元素个数一定能整除该有限群中元素的个数。因为 $2n$ 不能被 $n+1$ 整除，所以 $n$ 个反射操作再加上单位操作的集合不可能为 $D_n$ 的子群，也就是说两次反射操作的结合不为反射操作。

换句话说，因为 $2n$ 不能被 $n+1$ 整除，所以两次反射为旋转。

小结

用如此抽象的工具和复杂的流程来证明这样一个简单的结论并不是为了炫技，其背后的意义在于，对于一个群，其结构决定了其中的元素的性质。两个群如果有相同的结构，即同构（Isomorphism），那么它们之间对应元素的性质也是相同的。比如说，对于一个有着 $2p$ 个元素的非循环群（ $p$ 为一个素数），我们可以证明，它的非单位元素要么是 $2$ 阶的，要么是 $p$ 阶的，并且这个群与 $D_p$ 是同构的。因此，无需知道这个群对应的物理意义是什么，也可以立即得到结论：该群中任意两个 2 阶元素的结合一定为一个 $p$ 阶元素。