线性变换与矩阵乘法

在前面的章节中，我们指出矩阵 \(\mathbf{X} \in \mathbb{R}^{m \times n}\) 乘一个向量 \(\bm{v} \in \mathbb{R}^{n \times 1}\)，可以看作是将 \(\bm{v}\) 作为系数对矩阵 \(\mathbf{X}\)的列向量进行线性组合，得到一个新的 \(m\) 维向量。在本章，我们尝试从线性变换的角度重新理解这个过程。

线性变换的定义

设 \(V\) 和 \(W\) 是两个线性空间，如果存在一个映射 \(T: V \rightarrow W\)，使得对于任意的 \(x, y \in V\) 和任意的常数 \(\alpha\)，都有

1. 可加性：\(T(x + y) = T(x) + T(y)\)

2. 齐次性：\(T(\alpha x) = \alpha T(x)\)

那么我们称映射 \(T\) 是一个线性映射。

如果，一个线性映射是从一个线性空间到它自身的映射，即 \(T: V \rightarrow V\) ，那么我们称这个线性映射是一个线性变换。

对于一组基 \(\mathbf{X} \in \mathbb{R}^{n \times n}\)，定义如下的变换

\[ T(\bm{v}) = \mathbf{X} \bm{v}, \]

可以验证，变换 \(T\) 是一个线性变换：

1. 如果 \(\bm{v} \in \mathbb{R}^{n \times 1}\)，那么 \(T(\bm{v}) = \mathbf{X} \bm{v} \in \mathbb{R}^{n \times 1}\)
2. 可加性: \(T(\bm{v}_1 + \bm{v}_2) = \mathbf{X}(\bm{v}_1 + \bm{v}_2) = \mathbf{X} \bm{v}_1 + \mathbf{X} \bm{v}_2 = T(\bm{v}_1) + T(\bm{v}_2)\)
3. 齐次性: \(T(\alpha \bm{v}) = \mathbf{X} \alpha \bm{v} = \alpha \mathbf{X} \bm{v} = \alpha T(\bm{v})\)

二维线性变换

在这一小节，我们尝试以二维线性变换为例，从几何的角度来感受一下线性变换。根据上文的定义，我们知道一个二维的线性变换可以用一个 \(2 \times 2\)的矩阵来表示

\[ \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \end{bmatrix}. \]

这个矩阵可以将一个二维向量 \(\bm{v} = \begin{bmatrix} v_1 & v_2 \end{bmatrix}^{\mathrm{T}}\) 变换为另一个二维向量

\[ \bm{v}' = \mathbf{X} \bm{v} = \begin{bmatrix} x_{11} v_1 + x_{12} v_2 \\ x_{21} v_1 + x_{22} v_2 \end{bmatrix}. \]

于此同时，我们对于二维平面上的一些常见操作，比如旋转，缩放等等，都比较熟悉，那么这些操作如何用矩阵来表示呢？

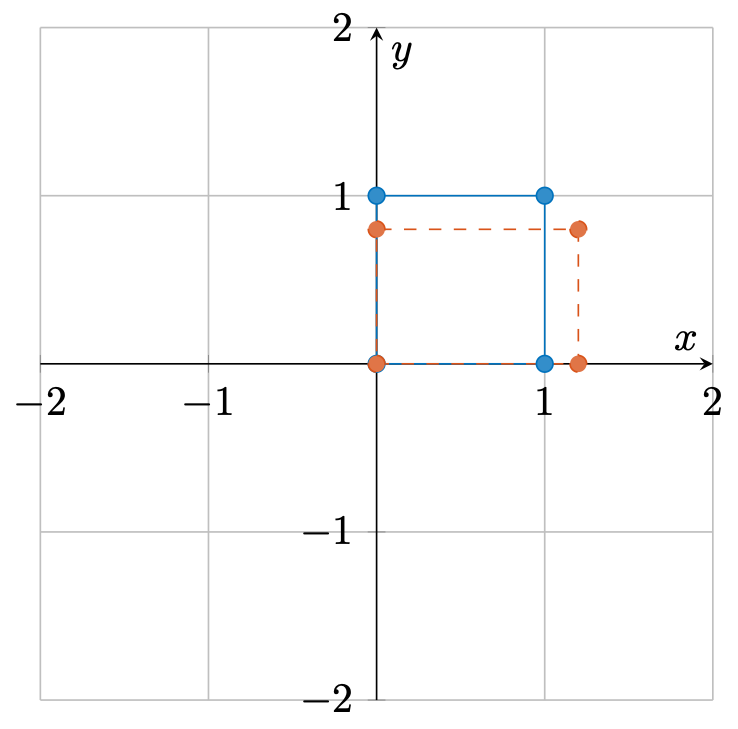
1. 缩放

   \[ \mathbf{X} = \begin{bmatrix} s_1 & 0 \\ 0 & s_2 \end{bmatrix}. \]

   可以发现，变换后的向量分别在两个方向上被缩放了 \(s_1, s_2\) 倍

   \[ \bm{v}' = \mathbf{X} \bm{v} = \begin{bmatrix} s_1 v_1 \\ s_2 v_2 \end{bmatrix}. \]

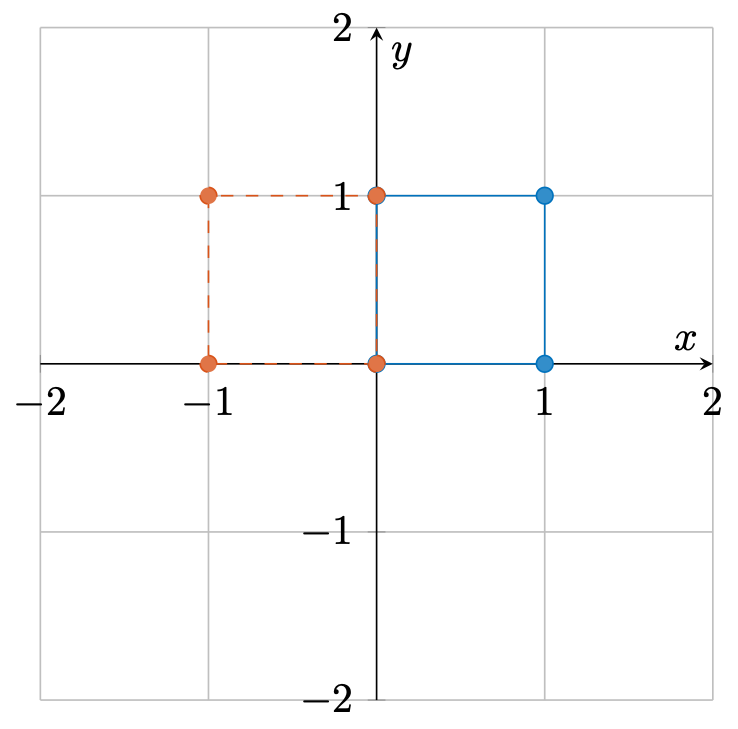
2. 反射

   \[ \mathbf{X} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}. \]

   此时，变换后的向量在第一个轴上被反转了

   \[ \bm{v}' = \mathbf{X} \bm{v} = \begin{bmatrix} -v_1 \\ v_2 \end{bmatrix}. \]

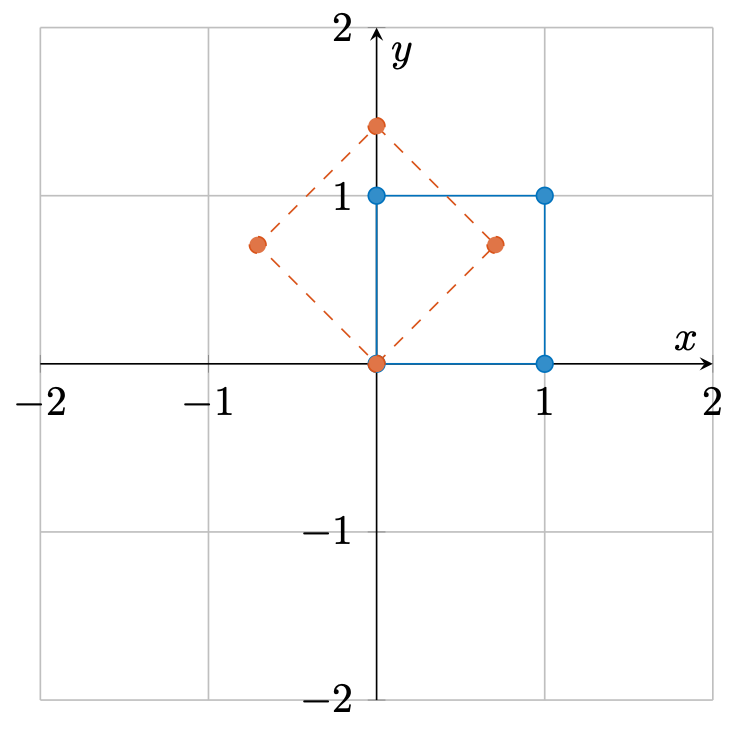
3. 旋转

   \[ \mathbf{X} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}. \]

   该矩阵相当将向量以原点为中心旋转了 \(\theta\) 度

   \[ \bm{v}' = \mathbf{X} \bm{v} = \begin{bmatrix} \cos \theta v_1 - \sin \theta v_2 \\ \sin \theta v_1 + \cos \theta v_2 \end{bmatrix}. \]

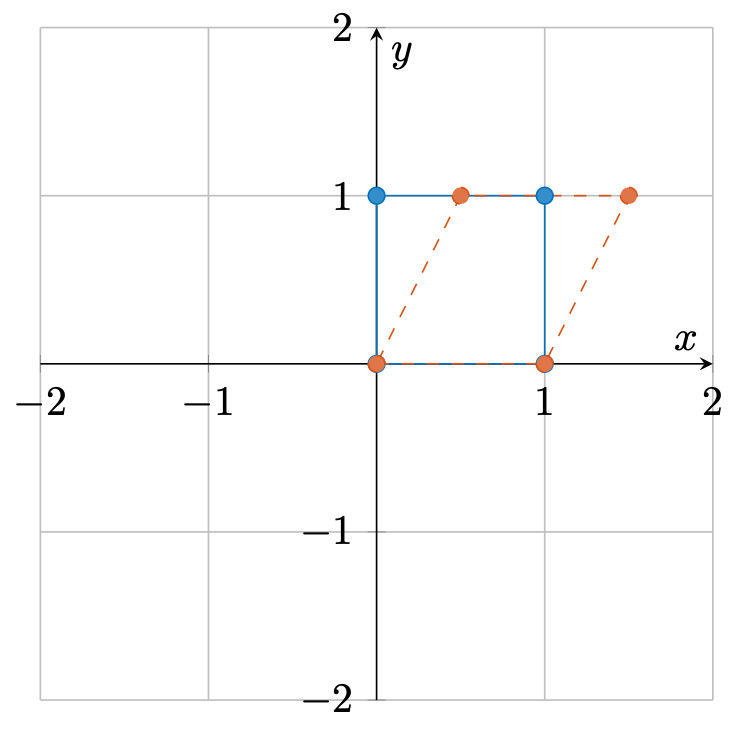
4. 剪切

   \[ \mathbf{X} = \begin{bmatrix} 1 & 0.5 \\ 0 & 1 \end{bmatrix}. \]

   此时，变换后的向量为

   \[ \bm{v}' = \mathbf{X} \bm{v} = \begin{bmatrix} v_1 + 0.5v_2 \\ v_2 \end{bmatrix}. \]

线性变换的组合

两个乃至多个线性变换的组合依旧是一个线性变换吗？这里我们简单证明一下，设有两个线性变换 \(T_1, T_2\) , 那么这两个线性变换的组合记作 \(T = T_1 \circ T_2\), 该变换满足

\[ T \bm{v} = (T_1 \circ T_2) \bm{v} = T_2(T_1(\bm{v})), \]

即线性变换的组合构成的新的变换 \(T\) 等价于先进行线性变换 \(T_1\) 然后再进行线性变换 \(T_2\)。可以验证

1. 如果 \(\bm{v} \in \mathbb{R}^{n \times 1}\)，那么 \(T_2(T_1(\bm{v})) \in \mathbb{R}^{n \times 1}\)
2. 可加性: \(T(\bm{v}_1 + \bm{v}_2) = T_2(T_1(\bm{v}_1 + \bm{v}_2)) = T_2(T_1(\bm{v}_1) + T_1(\bm{v}_2)) = T_2(T_1(\bm{v}_1)) + T_2(T_1(\bm{v}_2)) = T(\bm{v}_1) + T(\bm{v}_2)\)
3. 齐次性: \(T(\alpha \bm{v}) = T_2(T_1(\alpha \bm{v})) = T_2(\alpha T_1(\bm{v})) = \alpha T_2(T_1(\bm{v})) = \alpha T(\bm{v})\)

因此，\(T = T_1 \circ T_2\) 也是一个线性变换。设 \(T_1, T_2\)对应的变换矩阵分别为 \(\mathbf{A}, \mathbf{B} \in \mathbb{R}^{N \times N}\)，那么 \(T\) 对应的矩阵该有什么表达呢？

注意到，对于线性变换 \(T\) 我们有

\[ T(\bm{v}) = T_2(T_1(\bm{v})) = \mathbf{B}(\mathbf{A} \bm{v}). \]

令 \(A_{ij}, B_{ij}\) 为矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\) 的第 \(i\) 行，第 \(j\) 列元素，则有如下等式

\[ (\mathbf{A} \bm{v})_k = \sum_{i=1}^{N} A_{ki} v_i, \]

\[ (\mathbf{B}(\mathbf{A} \bm{v}))_k = \sum_{j=1}^{N} B_{kj} (\mathbf{A} \bm{v})_j = \sum_{j=1}^{n} B_{kj} \sum_{i=1}^{N} A_{ji} v_i = \sum_{i=1}^N \left(\sum_{j=1}^N B_{kj} A_{ji}\right) v_i. \tag{1} \]

设 \(T\) 对应的矩阵为 \(\mathbf{C}\)，则有

\[ T(\bm{v}) = \mathbf{C} \bm{v}, \]

变换后向量的第 \(k\) 个元素有如下表达式

\[ (\mathbf{C} \bm{v})_k = \sum_{i=1}^{N} C_{ki} v_i, \tag{2} \]

对比式 (1) 和式 (2) 可知，变换矩阵 \(\mathbf{C}\) 中的元素有如下表达式

\[ C_{ki} = \sum_{j=1}^{N} B_{kj} A_{ji}. \]

为了表达美观，我们可以将对应的变量进行替换，得到如下表达式

\[ C_{ij} = \sum_{k=1}^{N} B_{ik} A_{kj}. \tag{3} \]

我们将式 (3) 中的运算称作矩阵乘法，记作 \(\mathbf{C} = \mathbf{B} \mathbf{A}\)。

实际上，矩阵乘法可以这样计算，如 \(\mathbf{C} = \mathbf{B} \mathbf{A}\)，那么矩阵 \(\mathbf{C}\) 的第 \(i,j\) 个元素 \(\mathbf{C}_{ij}\)，为矩阵 \(\mathbf{B}\) 的第 \(i\) 行行向量 和矩阵 \(\mathbf{A}\) 的第 \(j\) 列列向量的内积。

此外，上文的推导都是基于方阵的（也就是行和列具有相同长度的矩阵）。对于一般的矩阵，同样可以使用矩阵乘法来计算，设有矩阵 \(\mathbf{A} \in \mathbb{R}^{M \times N}, \mathbf{B} \in \mathbb{R}^{N \times L}\)，那么这两个矩阵的乘积为

\[ \mathbf{C} = \mathbf{A} \mathbf{B} \in \mathbb{R}^{M \times L}. \]

可以看到，如果两个矩阵能够进行矩阵乘法，那么第一个矩阵的每一行都和第二个矩阵的每一列都有相同的长度。正是这样，矩阵乘法并不满足交换率，显然 \(\mathbf{A} \mathbf{B}\) 能够计算并不代表 \(\mathbf{B} \mathbf{A}\) 也能进行矩阵乘法。

小结

1. 线性变换可以用矩阵表示
2. 常见的线性变换就几何意义来说，有缩放、反射、旋转、剪切
3. 线性变换的组合可以用矩阵乘法表示