向量的基本运算

向量是向量空间中的一个元素，除了最基本的加法和数乘运算外，还有一些其他的运算。当然，正如向量空间有着明确的几何意义一样（比如二维向量空间是一个平面），这些运算我们同样也可以从几何的角度来理解。

当然，在介绍这些运算之前，我们先来回顾一下向量最基本的加法和数乘运算。设向量 \(\bm{x},\bm{y}\) 都为 \(n\) 维向量空间 \(V\) 中的元素，那么向量的加法运算定义为：

\[ \bm{x} + \bm{y} = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} + \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{bmatrix} = \begin{bmatrix} x_{1} + y_{1} \\ x_{2} + y_{2} \\ \vdots \\ x_{n} + y_{n} \end{bmatrix} \]

设 \(\alpha\) 为实数，那么向量的数乘运算定义为：

\[ \alpha \bm{x} = \alpha \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} \alpha x_{1} \\ \alpha x_{2} \\ \vdots \\ \alpha x_{n} \end{bmatrix} \]

向量的内积

内积是向量空间中最基本的运算之一，它不仅可以用来定义向量的长度，还可以用来定义向量之间的夹角。我们首先给出内积的定义。

给定两个 \(n\) 维向量 \(\bm{x}, \bm{y}\)，它们的内积定义为：

\[ \langle \bm{x}, \bm{y} \rangle = x_{1} y_{1} + x_{2} y_{2} + \cdots + x_{n} y_{n} = \sum_{i=1}^{n} x_{i} y_{i}. \]

简单来说，就是将两个向量对应位置的元素相乘，然后再将所有的乘积相加。并且，我们可以发现，内积满足如下性质：

\[ \langle \bm{x}, \bm{y} + \bm{z} \rangle = \langle \bm{x}, \bm{y} \rangle + \langle \bm{x}, \bm{z} \rangle. \]

那么，在给定内积的定义后，我们就可以进一步地给出向量的模长的计算公式：

\[ \|x\|^{2} = \langle \bm{x}, \bm{x} \rangle = x_{1}^{2} + x_{2}^{2} + \cdots + x_{n}^{2}. \]

换句话说就是，一个向量的模长的平方等于这个向量与自身的内积。

接下来，我们需要回忆一下三角形余弦公式：

\[ \|\bm{c}\|^{2} = \|\bm{a} - \bm{b}\|^{2} = \|\bm{a}\|^{2} + \|\bm{b}\|^{2} - 2 \|\bm{a}\| \|\bm{b}\| \cos \theta, \]

其中 \(\bm{a}, \bm{b}, \bm{c}\) 为三角形三个边，而\(\theta\) 为 \(\bm{a}\) 与 \(\bm{b}\) 的夹角。

与此同时，根据模长的计算公式，我们有

\[ \begin{split} \|\bm{a} - \bm{b}\|^{2} & = \langle \bm{a} - \bm{b}, \bm{a} - \bm{b} \rangle \\ & = \langle \bm{a}, \bm{a} \rangle + \langle \bm{b}, \bm{b} \rangle - 2 \langle \bm{a}, \bm{b} \rangle \\ & = \|\bm{a}\|^{2} + \|\bm{b}\|^{2} - 2 \langle \bm{a}, \bm{b} \rangle. \end{split} \]

对比上面两个公式，我们可以发现，两个向量之间的内积与它们的模长以及夹角之间存在着如下关系：

\[ \langle \bm{a}, \bm{b} \rangle = \|\bm{a}\| \|\bm{b}\| \cos \theta. \]

因此，两个向量之间的夹角可以通过如下公式计算：

\[ \cos \theta = \frac{\langle \bm{a}, \bm{b} \rangle}{\|\bm{a}\| \|\bm{b}\|}. \]

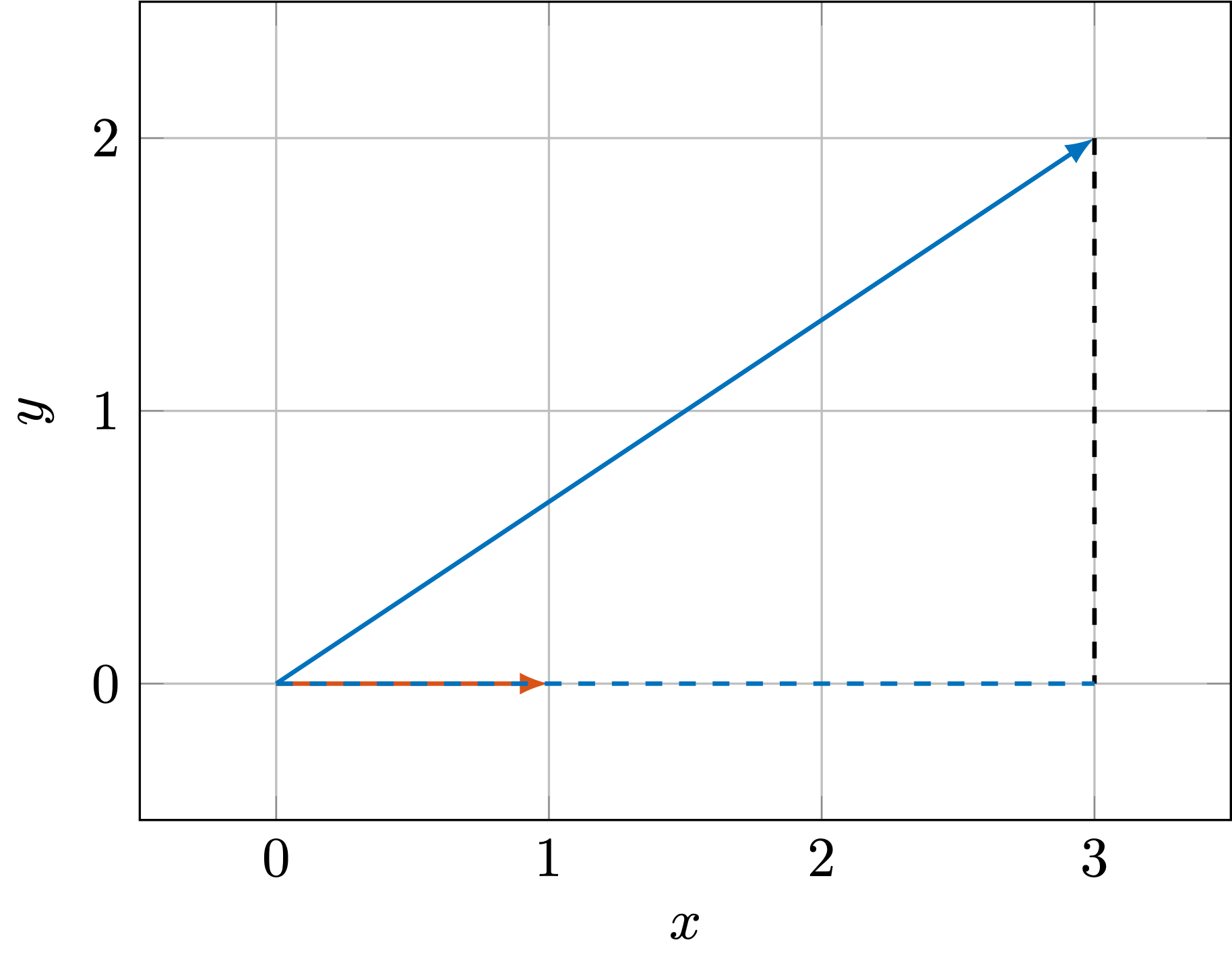
如此一来，向量的内积的几何意义就非常清晰了。不妨令向量 \(\bm{b}\) 的模长为 1，那么向量 \(\bm{a}\) 在向量 \(\bm{b}\) 上的投影长度就是 \(\|\bm{a}\| \cos \theta\)，而这就刚好等于 \(\langle \bm{a}, \bm{b} \rangle\)。

向量的线性组合

由于线性空间是加法和数乘封闭的，因此我们自然很关心多个向量以及他们的组合之间有什么联系。首先，我们先给出向量的线性组合的定义：

给定 \(m\) 个 \(n\) 维向量，\(\bm{x}_{1}, \bm{x}_{2}, \cdots, \bm{x}_{k} \in \mathbb{R}^{n \times 1}\)，以及一个 \(m\) 维列向量 \(\bm{v} = \begin{bmatrix} v_{1} & v_{2} & \cdots & v_{m} \end{bmatrix}^{\mathrm{T}}\)，那么这 \(m\) 个向量的线性组合定义为：

\[ \bm{y} = v_{1} \bm{x}_{1} + v_{2} \bm{x}_{2} + \cdots + v_{k} \bm{x}_{m}. \]

如果我们将这 \(m\) 个向量写成如下的形式：

\[ \begin{split} \mathbf{X} & = \begin{bmatrix} \bm{x}_{1} & \bm{x}_{2} & \cdots & \bm{x}_{m} \end{bmatrix}, \\ & = \begin{bmatrix} X_{11} & X_{12} & \cdots & X_{1m} \\ X_{21} & X_{22} & \cdots & X_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ X_{n1} & X_{n2} & \cdots & X_{nm} \end{bmatrix}, \end{split} \]

显然，\(X_{ij}\) 为向量 \(\bm{x}_{j}\) 的第 \(i\) 个元素，并且 \(\mathbf{X}\) 是一个有着 \(n \times m\) 元素的阵列，被称作矩阵。通常情况下，我们使用加粗的大写正体字母来表示矩阵，用如下的形式来标明矩阵的大小：

\[ \mathbf{X} \in \mathbb{R}^{n \times k}. \]

与此同时，矩阵与向量的乘法被定义为：

给定一个 \(n \times m\) 的矩阵 \(\mathbf{X}\)，以及一个 \(m\) 维向量 \(\bm{v}\)，那么矩阵与向量的乘法定义为：

\[ y_i = (\mathbf{X} \bm{v})_i = \sum_{j=1}^{m} X_{ij} v_{j}. \]

其中 \(y_i\) 为向量 \(\bm{y}\) 的第 \(i\) 个元素，\((\mathbf{X} \bm{v})_i\) 则表示矩阵乘以向量的结果的第 \(i\) 个元素。通常情况下，我们将矩阵与向量的乘法写成如下的形式：

\[ \bm{y} = \mathbf{X} \bm{v}. \]

尽管矩阵与向量的乘法看起来有些复杂，但是我们可以发现，矩阵与向量的乘法等价于向量的线性组合：一个矩阵 \(\mathbf{X} \in \mathbb{R}^{n \times m}\) 乘以一个向量 \(\bm{v} \in \mathbb{R}^{m\times 1}\)，实际上就是对矩阵的每一列进行线性组合，而向量 \(\bm{v}\) 中的每一个元素则是对应的线性组合的系数，即

\[ \bm{y} = \mathbf{X} \bm{v} = \begin{bmatrix} \bm{x}_1 & \bm{x}_2 & \cdots & \bm{x}_m \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_m \end{bmatrix} = v_{1} \bm{x}_{1} + v_{2} \bm{x}_{2} + \cdots + v_{k} \bm{x}_{m}. \]

特别地，当 \(\mathbf{X} = \bm{x}^{\mathrm{T}} = \begin{bmatrix} x_1 & x_2 & \cdots & x_m \end{bmatrix} \in \mathbb{R}^{1 \times m}\) 时，也就是矩阵 \(\mathbf{X}\) 实际上是一个行向量时，此时矩阵与向量的乘法就是向量的内积：

\[ y = \mathbf{X} \bm{v} = \sum_{i=1}^{m} x_i v_i = \langle \bm{x}, \bm{v} \rangle. \]

因此当给定两个维度相同的列向量\(x,y \in \mathbb{R}^{n \times 1}\)时，我们可以将它们的内积写成如下的形式：

\[ \langle \bm{x}, \bm{y} \rangle = \bm{x}^{\mathrm{T}} \bm{y}. \]

从几何的角度来说，向量的线性组合就是将一组向量拉伸或者压缩，然后再将它们相加。比如，图 2 中的两个向量

\[ \bm{x}_{1} = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, \quad \bm{x}_{2} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}. \]

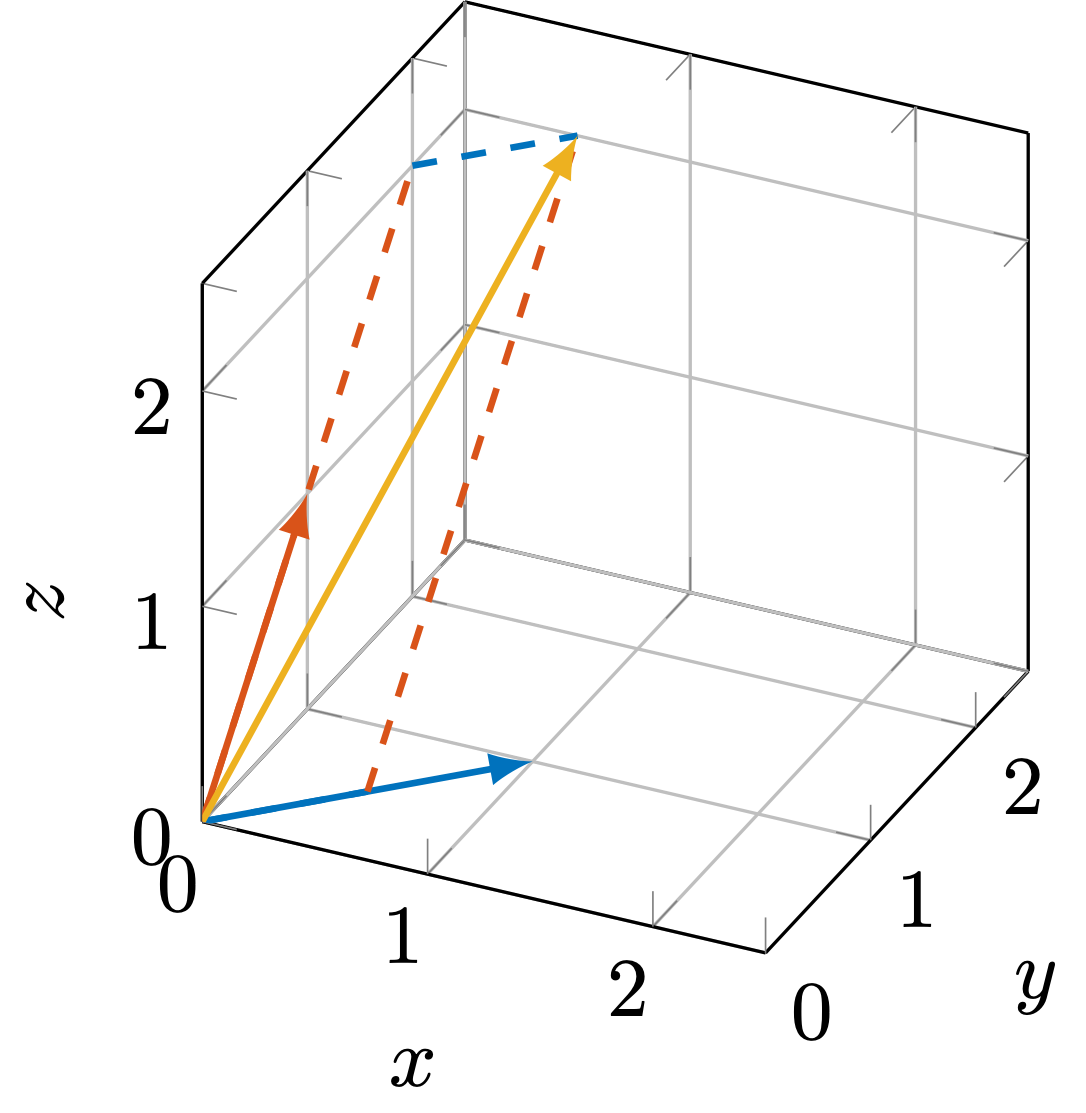
用组合系数 \(\bm{v} = \begin{bmatrix} 0.5 & 2 \end{bmatrix}^{\mathrm{T}}\)来对这两个向量进行线性组合，我们可以得到如下的结果：

\[ \bm{y} = 0.5\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} + 2\begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 2.5 \\ 2 \end{bmatrix}. \]

也就是图 2 中的黄色箭头所指示的向量。

小结

本节介绍了向量的内积以及向量的线性组合。向量的内积可以用来定义向量的模长以及向量之间的夹角，而向量的线性组合则引出了矩阵与向量的乘法。此外，对于这两种运算，我们还从几何的角度来理解了它们的意义。