分解多图匹配
图匹配(Graph Matching, GM)旨在两个图之间寻找一一对应的节点,而多图匹配(Multigraph Matching, MGM)则同时在多个图之间的匹配关系。在多图匹配中存在两个主要问题,即循环一致性问题和高时间和空间复杂度问题。一方面,基于两图的多图匹配方法具有低时间和空间复杂度,但为了保持匹配结果的循环一致性,需要引入额外的约束。此外,基于两图的多图匹配的精度高度依赖于所选优化算法。另一方面,基于张量的多图匹配方法可以避免循环一致性问题,但它们的时间和空间复杂度极高。在这篇论文中,我们发现在某些特定情况下基于两图的和基于张量的多图匹配方法是等价的。基于这一发现,我们提出了一种新的多图匹配方法,不仅避免了循环一致性问题,而且降低了复杂度。此外,我们通过引入多图匹配方法中亲和矩阵的无损分解进一步改进了该方法。相关论文已于 2021 年 9 月被期刊 Pattern Recognition 接收,全文可在这里下载。
研究背景
图匹配,旨在找到两个给定图之间的对应关系,是计算机视觉、模式识别、数据挖掘等领域中一个基础而具有挑战性的问题。在过去的几十年里,图匹配问题的研究非常广泛:图匹配模型从最简单的线性分配问题演变到二次分配问题(最常用),再到高阶匹配问题。线性分配问题的最优解可以在多项式时间内通过匈牙利方法获得。然而,二次分配问题和高阶匹配问题是已知的 NP 难问题。因此,许多算法被提出来有效地获得它们的近似解。此外,还有一些研究针对图匹配问题的高时间和空间复杂度进行了改进。近年来,研究人员将他们的关注点转向了多图匹配问题,该问题旨在同时建立两个以上图之间的对应关系。
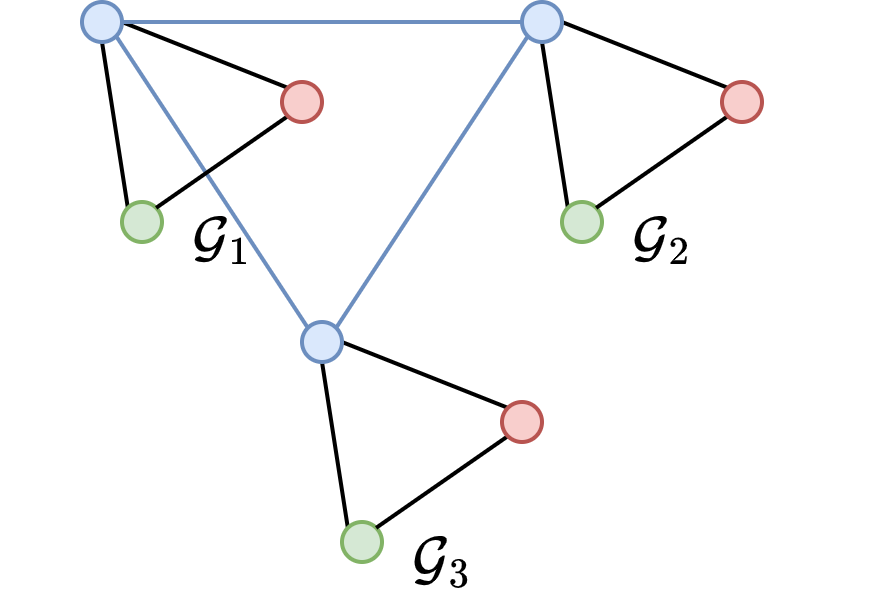
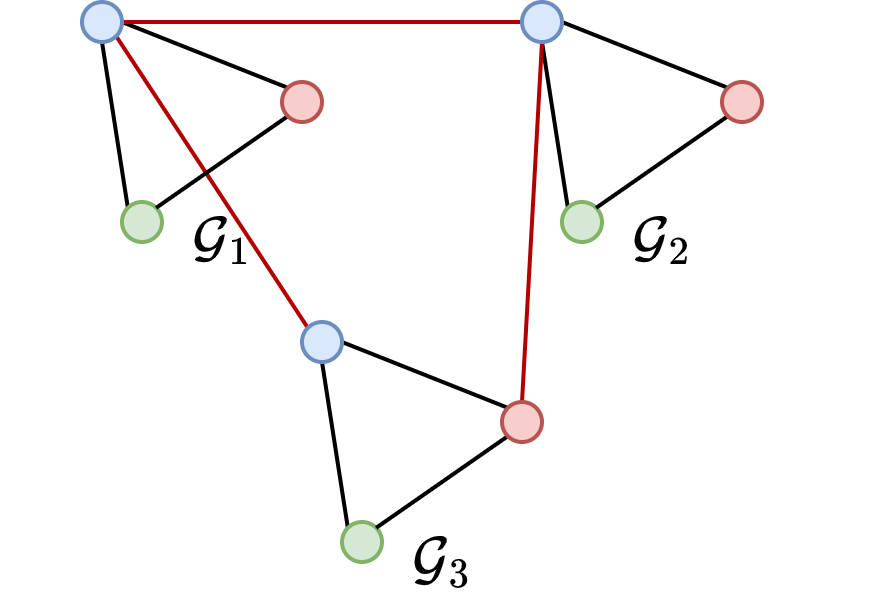
在 MGM 中,一个主要任务是确保解是循环一致的。例如,如果节点\(a\)对应于节点\(b\),并且\(b\)对应于节点\(c\),那么节点\(a\)必须对应于节点\(c\)。可以看到在图 1.1a 中,匹配结果是循环一致的,相反,在图 1.1b 中,循环一致性在匹配结果中并不满足。显然,当在 MGM 中使用基于两图匹配方法时,两两独立计算的两图匹配结果可能是循环不一致的。因此,许多 MGM 方法被提出来解决这个问题,它们大部分可以分为两类:单次方法和迭代方法。单次方法试图直接从其他两图匹配方法获得的匹配结果中提取一个循环一致的解。但由于不会进一步优化目标函数,这些方法通常对输入很敏感。而迭代方法则在最大化 MGM 的目标函数同时兼顾循环一致性。部分迭代方法中,整个迭代过程严格遵守循环一致性,也有部分方法在迭代过程中逐渐增加循环一致性的重要性。
注意到,上述方法都是基于两图图匹配的,因此,保证匹配结果的循环一致性成为它们不可避免的任务。最近,有研究者引入了一个张量形式的目标函数表达式,自然地避免了循环一致性问题。不幸的是,该方法的时间和空间复杂度极高。因此,在实现过程中,作者仅将张量形式应用于 MGM 目标函数中的一阶(节点到节点相似性)部分。此外,一个简化的基于两图图匹配的 MGM 模型被用来表示二阶(边到边相似性)部分的目标函数,从而使整个算法时间和空间复杂度在实际应用中是接受的。
尽管基于两图的 MGM 和基于张量的 MGM 在表达式上看似不同,但令人惊讶的是,前者可以其实是后者的一个特例。这一发现表明循环一致性问题在基于两图的 MGM 方法中同样是可以避免的。此外,我们希望通过利用模型中亲和矩阵的稀疏性,进一步降低所提方法的复杂性。并且,由于 MGM 中的整数约束,目标函数存在许多局部极值。因此,本文提出的方法采用了类似于随机梯度下降方法的优化方法,大大缓解了局部极值问题。
背景知识
一般情况下,图由一组节点和边构成,用符号 \(\mathcal G = \{ \mathcal V, \mathcal E \}\) 表示,其中 \(\mathcal V\) 表示节点集合,\(\mathcal E\) 表示边。此外,图 \(\mathcal G\) 中的节点数为 \(n_v = \lvert \mathcal V \rvert\),边数为 \(n_e = \lvert \mathcal E \rvert\)。此外,在本文中,图 \(\mathcal G\) 还关联着 \(4\) 个关联矩阵:\(\mathbf H^{11} \in \{0, 1\}^{n_v \times n_v}, \mathbf H^{12} \in \{0, 1\}^{n_v \times n_e}, \mathbf H^{21} \in \{0, 1\}^{n_e \times n_v}, \mathbf H^{22} \in \{0, 1\}^{n_e \times n_e}\)。关联矩阵 \(\mathbf H^{ab}\) 用于表示 \(a^{th}\)-阶 特征和 \(b^{th}\)-阶 特征之间的连接关系。例如,如果第 \(i^{th}\) 二阶特征(第 \(i^{th}\) 条边)与第 \(j^{th}\) 一阶特征(第 \(j^{th}\) 个节点)相连,则 \(\mathbf H^{21}_{ij}\) 被设置为 1。此外,在多图集合中,对于第 \(k^{th}\) 图 \(\mathcal G^{[k]}\),它的节点数和边数分别用 \(n^{[k]}_v\) 和 \(n^{[k]}_e\) 表示。\(\mathcal G^{[k]}\) 的关联矩阵以 \(\mathbf H^{[k]^{ab}}\) 的形式给出。
给定 \(m\) 个图,大多数多图匹配(MGM)方法的目标函数如下:
\[ \begin{aligned} \hat{\mathbf{X}}^{[pq]} = & \mathop{\arg\max}\limits_{\mathbf{X^{[pq]}}} \sum_{p, q, p \neq q} vec(\mathbf X^{[pq]})^{\rm T} \mathbf K^{[pq]} vec(\mathbf X^{[pq]}) & \\ \text{s.t. } & \mathbf X^{[pq]} \bm 1^{[q]} = \bm 1^{[p]}, (\mathbf X^{[pq]})^{\rm T}\bm 1^{[p]} \leq \bm 1^{[q]}, \\ & \mathbf X^{[pq]} \in \{0, 1\}^{n^{[p]}_v\times n^{[q]}_v}, \mathbf X^{[pr]} \mathbf X^{[rq]} = \mathbf X^{[pq]}, & \end{aligned} \]
其中带有 \(^{[pq]}\) 上标的符号是 \(\mathcal G^{[p]}\) 和 \(\mathcal G^{[q]}\) 的对应变量。例如,\(\mathbf K^{[pq]} \in \mathbb R^{n^{[p]}_vn^{[q]}_v \times n^{[p]}_vn^{[q]}_v}\) 是 \(\mathcal G^{[p]}\) 和 \(\mathcal G^{[q]}\) 之间的关联矩阵。可以发现该目标函数等价于最大化两图图匹配问题的所有目标函数的总和。此外,\(\mathbf X^{[pr]} \mathbf X^{[rq]} = \mathbf X^{[pq]}\) 确保了匹配结果的循环一致性。
迭代方法在整个变量更新过程中考虑了循环一致性约束,对应的目标函数为:
\[ \begin{split} & \sum_{p, q, p \neq q} vec(\mathbf X^{[pr]} \mathbf X^{[rq]} )^{\rm T} \mathbf K^{[pq]} vec(\mathbf X^{[pr]} \mathbf X^{[rq]}) \\ = & \sum_{p} vec(\mathbf X^{[pr]})^{\rm T} (\sum_{q, q \neq p} (\mathbf X^{[qr]} \otimes \mathbf I)^{\rm T} \mathbf K^{[pq]} (\mathbf X^{[qr]} \otimes \mathbf I)) vec(\mathbf X^{[pr]}), \end{split} \]
其中 \(\mathbf{I}\) 是单位矩阵。然后,对于特定的 \(\mathbf X^{[pr]}\),解可以通过求解具有 \(\mathbf K'^{[pr]} = \sum*{q, q \neq p} (\mathbf X^{[qr]} \otimes \mathbf I)^{\rm T} \mathbf K^{[pq]} (\mathbf X^{[qr]} \otimes \mathbf I)\) 亲和矩阵的两图匹配问题来获得。需要注意的是,在迭代过程中,当 \(\{\mathbf X^{[qr]} | q \neq r\}\) 中的任何元素发生变化时,亲和矩阵 \(\mathbf K'^{[pr]}\) 需要重新生成,以确保循环一致性。
同时,单次方法独立优化每个两图图匹配问题,并获得一个收集所有两图结果的矩阵 \(\mathbf W\),即
\[ \mathbf W = \begin{bmatrix} \mathbf X^{[11]} & \cdots & \mathbf X^{[1m]} \\ \vdots & \ddots & \vdots \\ \mathbf X^{[m1]} & \cdots & \mathbf X^{[mm]} \\ \end{bmatrix}. \]
需要注意的是,如果满足循环一致性,矩阵 \(\mathbf W\) 可以分解为\(\mathbf W = \mathbf U^{\rm T} \mathbf U,\) 其中 \(\mathbf U = [\mathbf X^{[11]}, \cdots, \mathbf X^{[1m]}]\)。大多数单次方法利用 \(\mathbf W\) 的低秩特性,并尝试从其他两图匹配方法的结果中重建一个满足循环一致性的 \(\mathbf W\)。可以发现,在获得 \(\mathbf W\) 后,亲和矩阵不再参与进一步的计算。因此,单次方法通常具有较低的计算复杂度。然而,在单次方法中,没有进一步优化 MGM 的目标函数。因此,当使用相同的两图匹配方法时,单次方法的性能通常不如迭代方法。
最近,有研究者提出了 MGM 问题的张量形式,自然地避免了循环一致性问题。设 \(\mathcal X \in \{0, 1\}^{n_v^{[1]} \times n_v^{[2]} \times \cdots \times n_v^{[m]}}\) 为指示张量,\(\mathcal X_{i_1:i_m} = 1\) 表示 \(\mathcal G^{[1]}\) 中的第 \(i_1\) 个节点、\(\dots\)、\(\mathcal G^{[m]}\) 中的第 \(i_m\) 个节点被匹配。注意,下标 \(_{i_1:i_m}\) 是 \(_{i_1, i_2, \cdots, i_m}\) 的简写,\(\mathcal X_{i_1:i_m}\) 是张量 \(\mathcal X\) 中索引为 \(i_1, i_2, \cdots, i_m\) 的元素。然后,基于张量的 MGM 可以如下表述(不失一般性,假设第一个图的节点数最小)。
\[ \begin{aligned} \hat{\mathcal{X}} = & \mathop{\arg\max}\limits_{\mathcal{X}} \sum_{i_1:i_m} \mathcal S_{i_1:i_m} \mathcal X_{i_1:i_m} + \sum_{i_1:i_m, j_1:j_m} \mathbf K_{i_1:i_m, j_1:j_m} \mathcal X_{i_1:i_m} \mathcal X_{j_1:j_m} & \\ = & \mathop{\arg\max}\limits_{\mathcal{X}}\ vec(\mathcal S)^{\rm T} vec(\mathcal X) + vec(\mathcal X)^{\rm T} \mathbf K vec(\mathcal X) & \\ \text{s.t. } & \mathcal X \in \{0, 1\}^{n_v^{[1]} \times n_v^{[2]} \times \cdots \times n_v^{[m]}}, & \\ & \mathcal X \times_2 \mathbf 1^{[2]} \cdots \times_m \mathbf 1^{[m]} = \mathbf 1^{[1]}, & \\ & \mathcal X \times_1 \mathbf 1^{[1]} \cdots \times_m \mathbf 1^{[m]} \leq \mathbf 1^{[2]}, \\ & \cdots, & \\ & \mathcal X \times_1 \mathbf 1^{[1]} \cdots \times_{m-1} \mathbf 1^{[m-1]} \leq \mathbf 1^{[m]}, & \end{aligned} \]
其中 \(\mathcal S \in \mathbf R^{n_v^{[1]} \times \cdots \times n_v^{[m]}}\) 是节点相似性张量,\(\mathbf K \in \mathbf R^{(n_v^{[1]}\cdots n_v^{[m]}) \times (n_v^{[1]}\cdots n_v^{[m]})}\) 是 MGM 中的亲和矩阵。在 \cref{eq:tmgm} 中,\(\times_k\) 表示张量 \(\mathcal A \in \mathbb R^{I_1 \times I_2 \times \cdots \times I_K}\) 与矩阵 \(\mathbf B \in \mathbb R^{I_k \times J}\) 的 \(k\) 模乘积,定义如下
\[ (\mathcal A \times_k \mathbf B)_{i_1 \cdots j \cdots i_{N}} = \sum_{i_k=1}^{I_k} \mathcal A_{i_1 \cdots i_k \cdots i_{K}} \mathbf B_{i_k j}. \]
此外,如果 \(\mathbf K_{i_1:i_m, i_1:i_m}\)(对角元素)等于 \(\mathcal S_{i_1:i_m}\),目标函数的两个部分可以合并为一个部分,即 \(vec(\mathcal X)^{\rm T} \mathbf K vec(\mathcal X)\)。
方法介绍
假设对于所有要匹配的 \(m\) 个图,存在一个虚拟图 \(\mathcal G^{[0]}\),其具有 \(n_v^{[0]} = \min(n_v^{[1]}, \cdots, n_v^{[m]})\) 个节点,且 \(\mathcal G^{[0]}\) 与 \(\mathcal G^{[i]}\) 之间的指示矩阵为 \(\mathbf X^{[0i]} \in \{0, 1\}^{n_v^{[0]} \times n_v^{[i]}}\)。类似地,\(\mathbf X^{[i0]} = \mathbf X^{[0i]^{\rm T}}\) 是 \(\mathcal G^{[i]}\) 与 \(\mathcal G^{[0]}\) 之间的指示矩阵。然后,对于总体指示张量 \(\mathcal X\),我们有以下定理:
定理 1: 设 \(\mathbf X^{[0i]}\) 是虚拟图 \(\mathcal G^{[0]}\) 与第 \(i\) 个图 \(\mathcal G^{[i]}\) 之间的指示矩阵,那么对于所有 \(m\) 个图的指示张量 \(\mathcal X\) 可以如下因式分解:
\[ \mathcal X = \mathcal I \times_1 \mathbf X^{[01]} \times_2 \mathbf X^{[02]} \cdots \times_m \mathbf X^{[0m]}, \]
其中 \(\mathcal I\) 是一个大小为 \(n_v^{[0]} \times n_v^{[0]} \times \cdots \times n_v^{[0]}\) 的对角线张量,对角元素全部为 1。
根据定理 1,在亲和矩阵 \(\mathbf K\) 被特别构建的情况下,基于张量的 MGM 的目标函数可以写成两图形式:
定理 2: 当在基于张量的 MGM 中,亲和矩阵 \(\mathbf K\) 被特别构建如下时
\[ \mathbf K_{i_1:i_m, j_1:j_m} = \sum_{p, q, p \neq q}\mathbf K^{[pq]}_{i_p i_q, j_pj_q} \]
其中 \(\mathbf K^{[pq]}\) 是 \(\mathcal G^{[p]}\) 和 \(\mathcal G^{[q]}\) 之间的亲和矩阵。那么,基于张量的 MGM 中的目标函数可以写成如下形式
\[ vec(\mathcal X)^{\rm T} \mathbf K vec(\mathcal X) = \sum_{p, q, p \neq q} vec(\mathbf X^{[p0]} \mathbf X^{[0q]})^{\rm T} \mathbf K^{[pq]} vec(\mathbf X^{[p0]} \mathbf X^{[0q]}). \]
可以发现,如果选择虚拟图为 \(\mathcal G^{[r]}\),此时基于张量的 MGM 的目标函数与基于两图的 MGM 的目标函数完全相同,因此,基于两图的 MGM 实际上是基于张量的 MGM 的特殊情况。进一步地,通过引入亲和矩阵的无损分解,并设 \(\mathbf U = [\mathbf X^{[01]}, \cdots, \mathbf X^{[0m]}]\) 是包含所有解的矩阵,则 MGM 问题的目标函数可以写成如下形式:
\[ \begin{split} J(\mathbf U) = \sum_{p, q, p \neq q} vec(\mathbf D^{[pq]})^{\rm T} vec(\mathbf V^{[p]^{\rm T}} \mathbf X^{[p0]} \mathbf X^{[0q]} \mathbf V^{[q]})^{\circ 2}, \end{split} \]
其中
\[ \mathbf D^{[pq]} = \begin{bmatrix} \mathbf T^{[pq]} & -\mathbf T^{[pq]} \mathbf H^{[q]^{21}} \\ -\mathbf H^{[p]^{12}} \mathbf T^{[pq]} & \mathbf H^{[p]^{12}} \mathbf T^{[pq]} \mathbf H^{[q]^{21}} + \mathbf S^{[pq]} \end{bmatrix}, \]
且 \(^{\circ 2}\) 表示对 2 进行逐元素平方。在这种情况下,\(J(\mathbf U)\) 对 \(\mathbf X^{[p0]}\) 的梯度为
\[ \begin{split} & \nabla \mathbf X^{[p0]} = 2\sum_{q, q \neq p}\mathbf V^{[p]}(\mathbf D^{[pq]} \circ (\mathbf V^{[p]^{\rm T}} \mathbf X^{[p0]} \mathbf X^{[0q]} \mathbf V^{[q]})) \mathbf V^{[q]^{\rm T}} \mathbf X^{[q0]}, \end{split} \]
其中 \(\circ\) 表示逐元素相乘。算法流程如下:
输入: 要匹配的 \(m\) 张图,虚拟图的索引 \(r\),以及相应的匹配结果 \(\mathbf U\)
输出: 两图匹配结果 \(\mathbf W\)
备份解: \(\mathbf U' = \mathbf U\)
重复以下步骤,直到 \(\mathbf U\) 收敛(全局更新)
对于 \(p = 1:m\) 且 \(p \neq r\)
使用 RRWM(Reweighted Random Walk Matching)根据全局梯度 \(\nabla \mathbf X^{[p0]}\) 更新 \(\mathbf X^{[p0]}\)
如果 \(\mathbf U \neq \mathbf U'\) 且 \(J(\mathbf U) < J(\mathbf U')\)
- 恢复之前的结果: \(\mathbf U = \mathbf U'\)
否则
- 备份解: \(\mathbf U' = \mathbf U\)
重复以下步骤,直到 \(\mathbf U\) 收敛(局部更新)
对于 \(p = 1:m\) 且 \(p \neq r\)
对于 \(q = 1:m\) 且 \(q \neq p\)
使用 RRWM 根据局部梯度 \(\nabla \mathbf X^{[p0]}_q\) 更新 \(\mathbf X^{[p0]}\)
如果 \(\mathbf U \neq \mathbf U'\) 且 \(J(\mathbf U) < J(\mathbf U')\)
- 恢复之前的结果: \(\mathbf U = \mathbf U'\)
否则
- 备份解: \(\mathbf U' = \mathbf U\)
通过 \(\mathbf W = \mathbf U^{\rm T} \mathbf U\) 计算 \(\mathbf W\)
实验结果
仿真实验
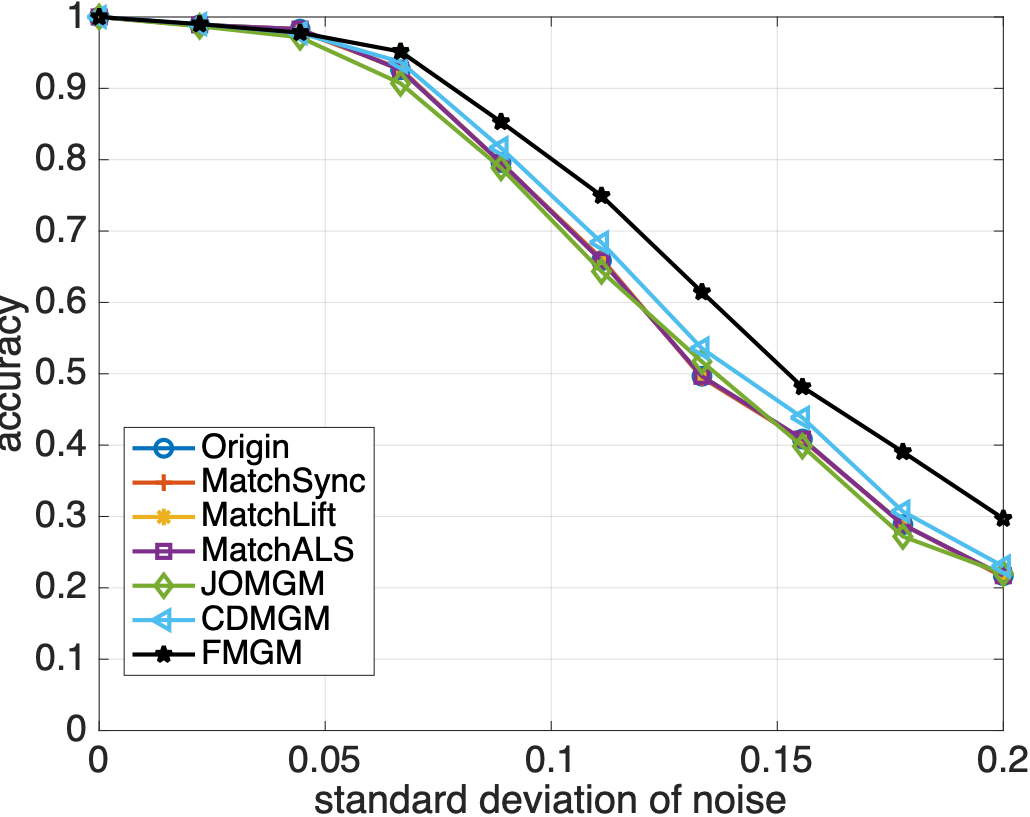
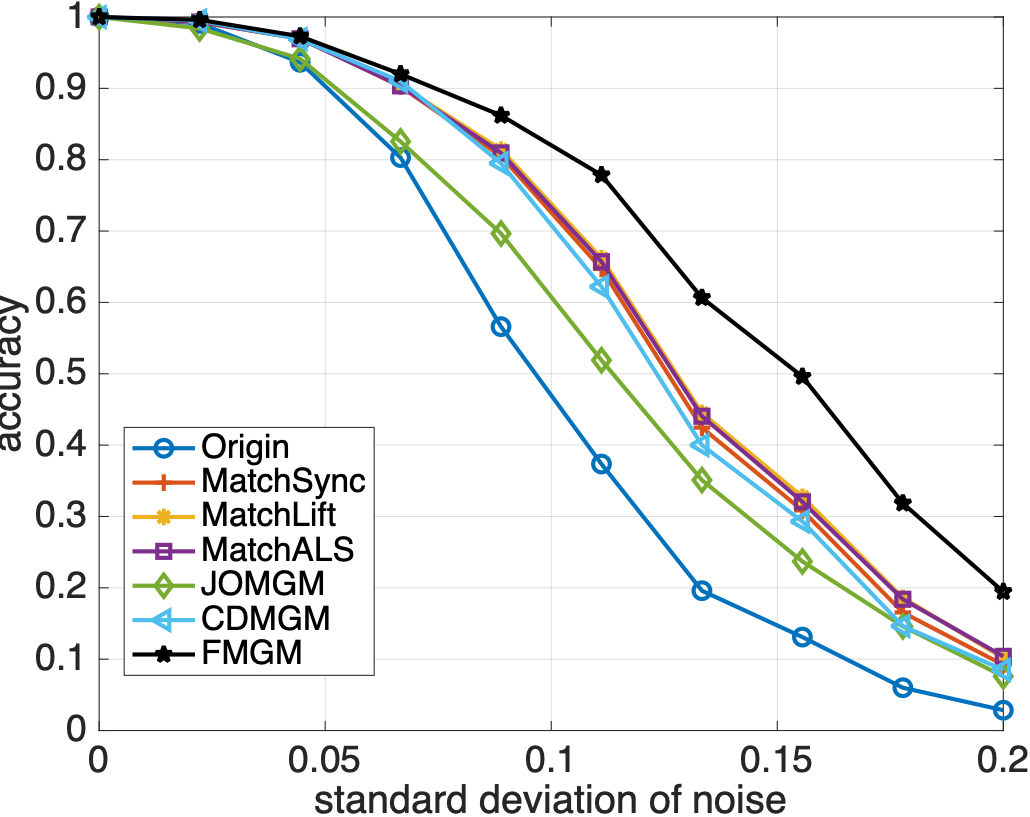
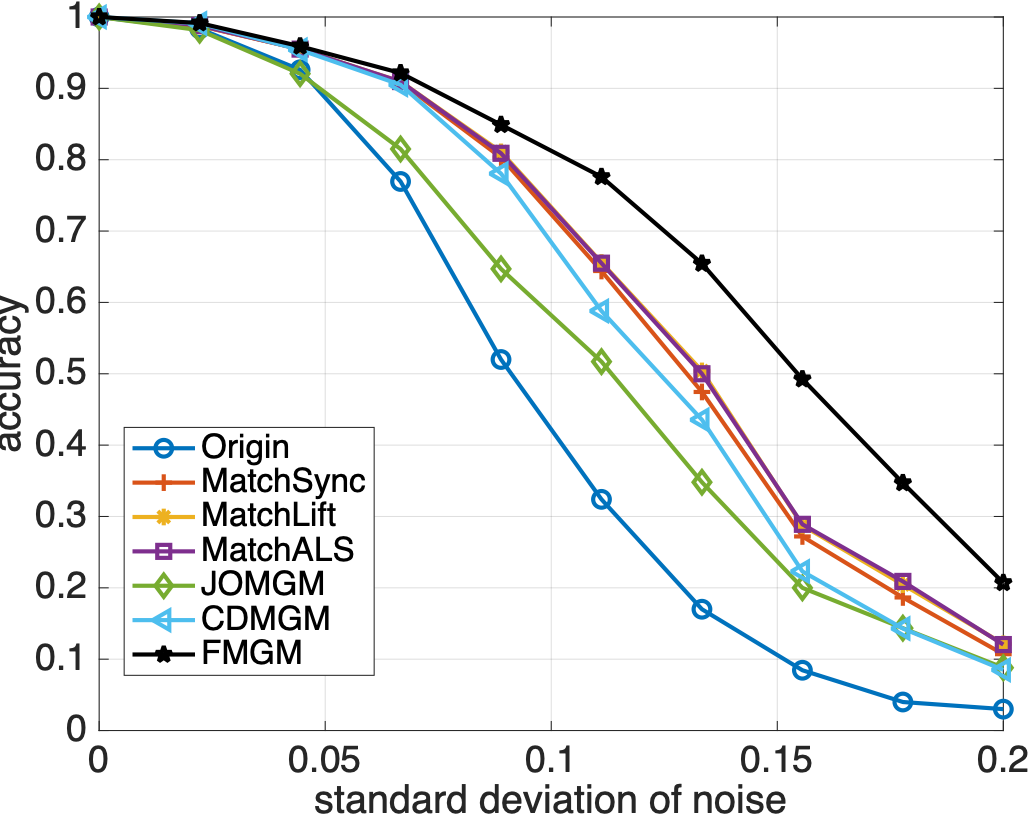
随机生成多个图并添加噪声,各算法匹配精度如下:
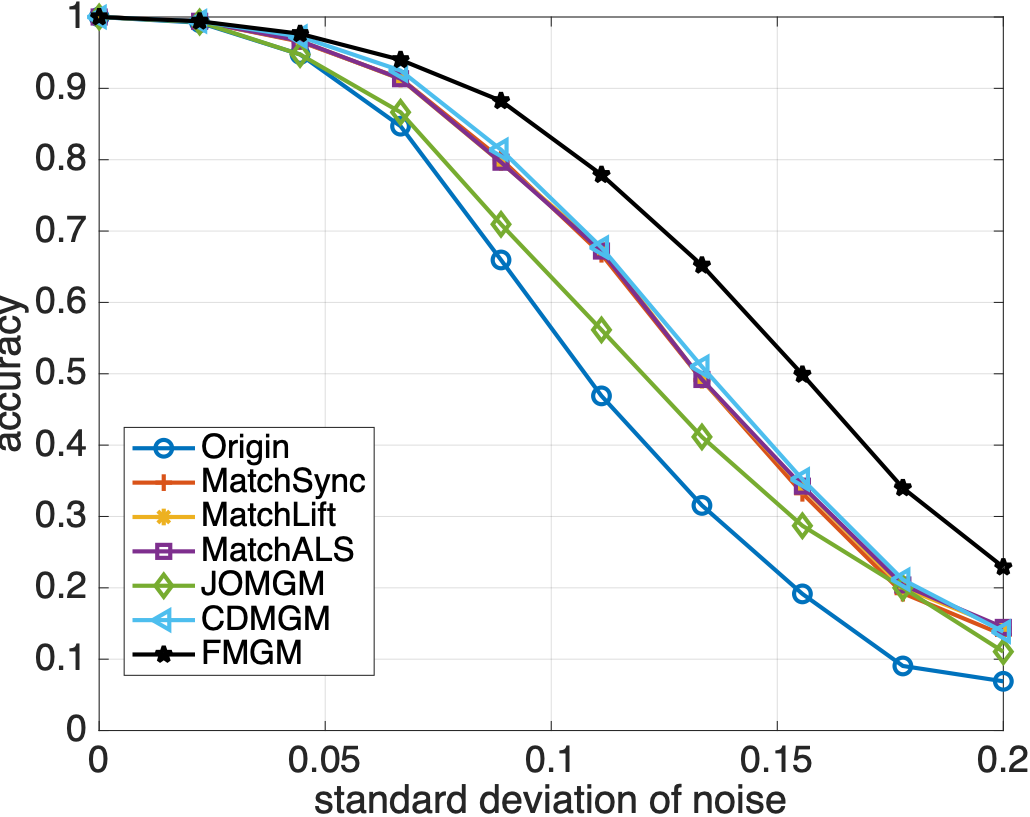
同样随机生成多个图并添加异常点,各算法匹配精度如下:
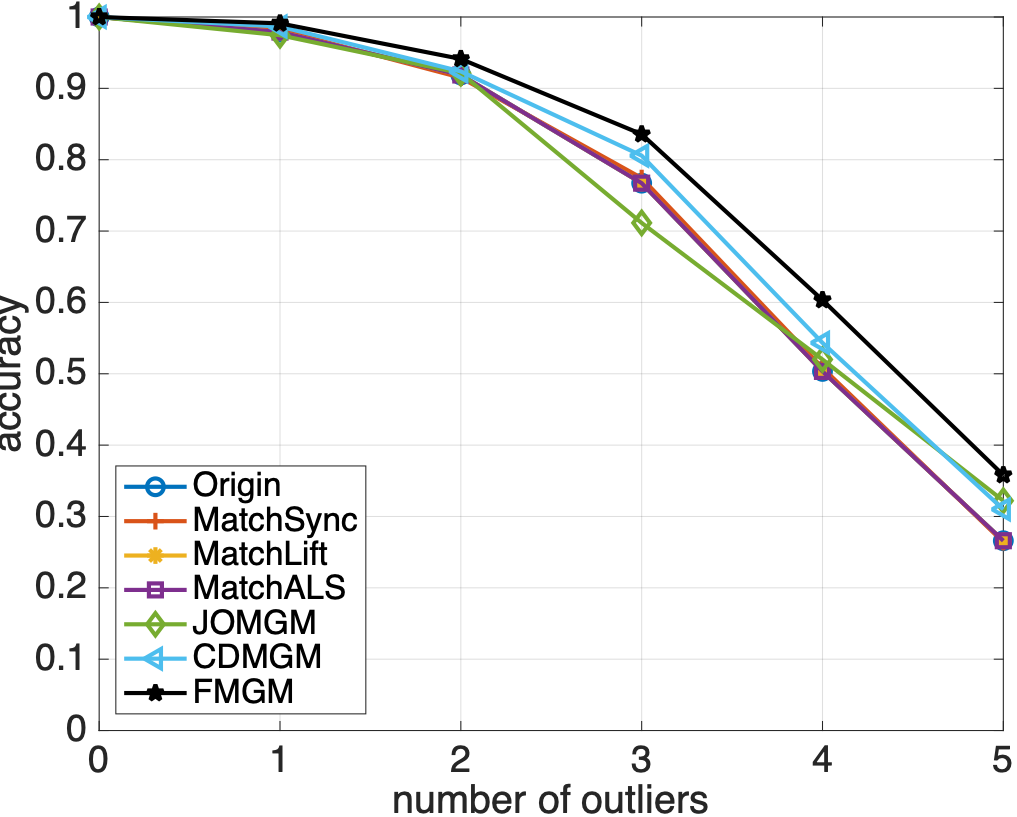
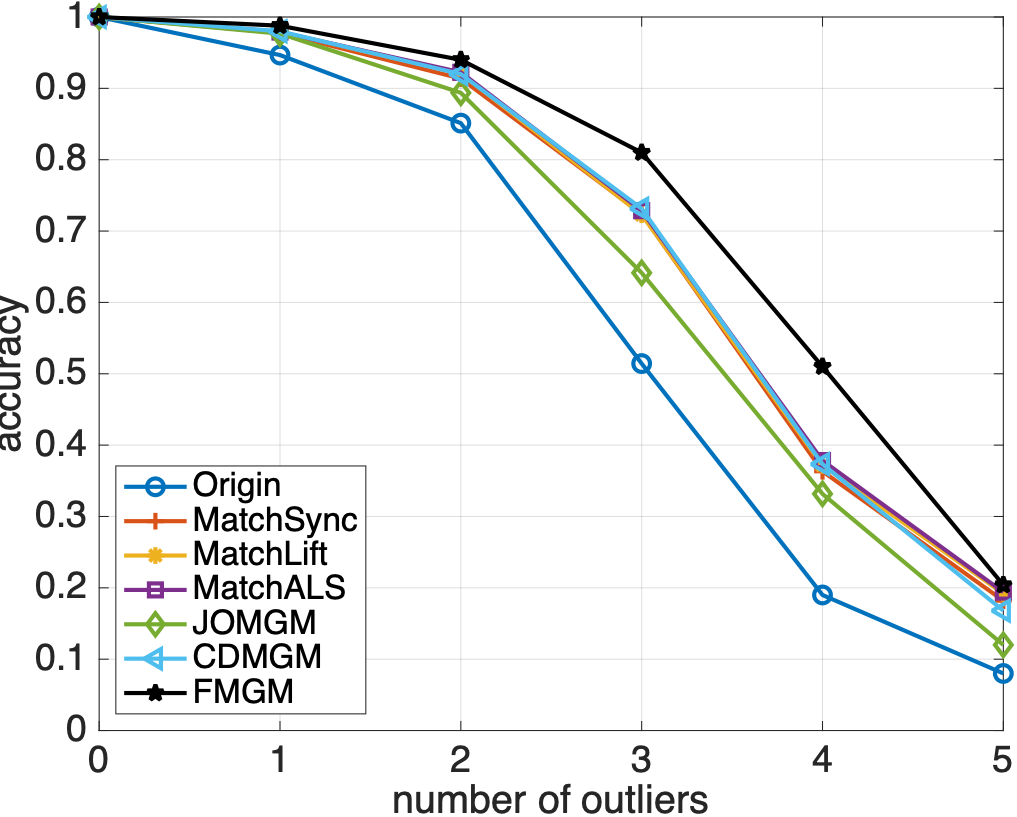
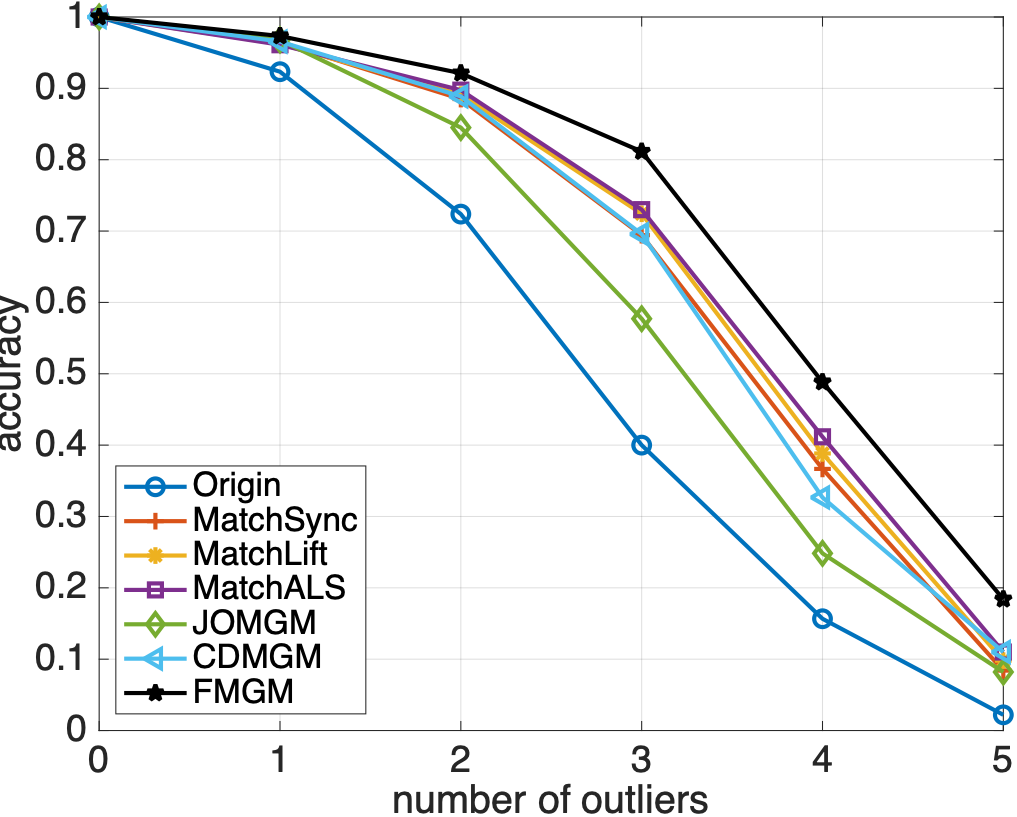
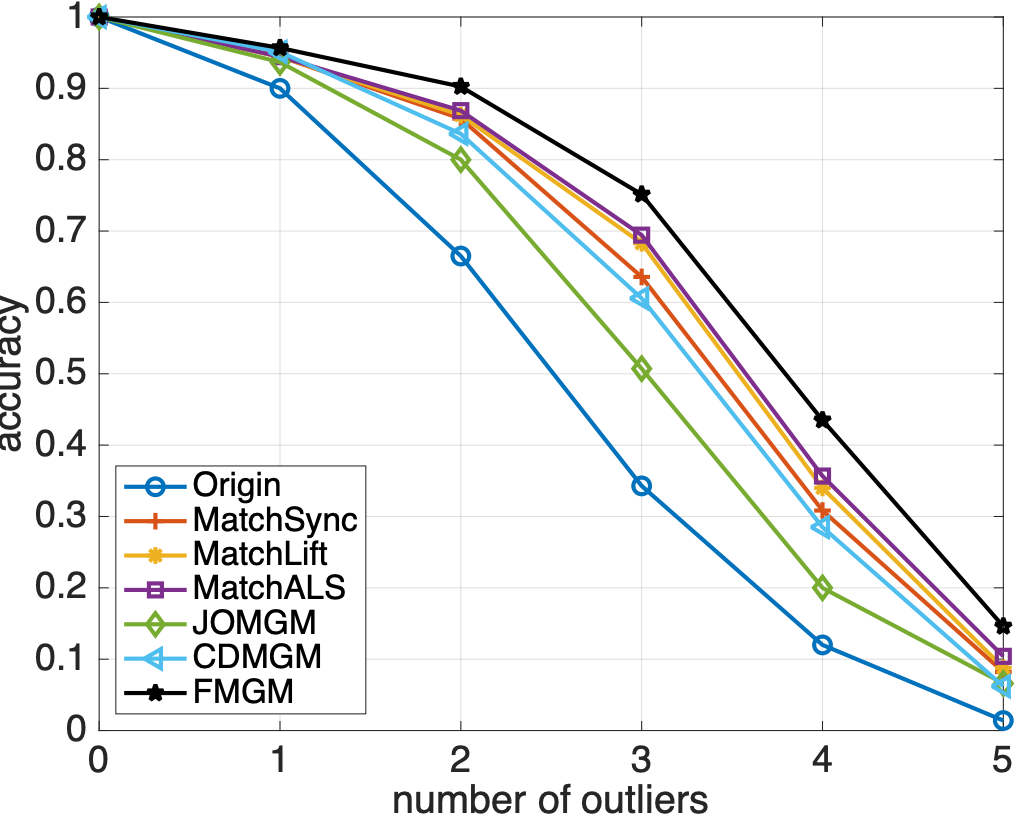
从图 2 和 3 中可以看到,与主流算法相比,本文提出的算法 FMGM 具有最好的抗噪声和抗异常点性能。
VOC 数据集实验
VOC 数据集包含来自 20 个类别的共 10,103 张图像,并且在每个类别中,每张图像都包含了 2 到 10 个特定关键点。VOC 数据集的部分图像如下所示。
.png)
.png)
匹配精度见下表:
| Origin | MatchSync | MatchLift | MatchALS | JOMGM | CDMGM | FMGM | |
|---|---|---|---|---|---|---|---|
| plane | 0.2655 | 0.258 | 0.2655 | 0.2655 | 0.3095 | 0.291 | 0.304 |
| bicycle | 0.156 | 0.1495 | 0.156 | 0.156 | 0.172 | 0.1635 | 0.1675 |
| bird | 0.152 | 0.1555 | 0.152 | 0.152 | 0.192 | 0.1665 | 0.1725 |
| boat | 0.184 | 0.184 | 0.184 | 0.184 | 0.188 | 0.1845 | 0.2085 |
| bottle | 0.1235 | 0.11 | 0.1235 | 0.1235 | 0.1225 | 0.124 | 0.1235 |
| bus | 0.59 | 0.563 | 0.59 | 0.59 | 0.6515 | 0.671 | 0.6785 |
| car | 0.308 | 0.307 | 0.308 | 0.308 | 0.3365 | 0.318 | 0.337 |
| cat | 0.732 | 0.727 | 0.732 | 0.732 | 0.7855 | 0.7605 | 0.788 |
| chair | 0.3205 | 0.3115 | 0.3205 | 0.3205 | 0.373 | 0.381 | 0.4005 |
| cow | 0.782 | 0.78 | 0.782 | 0.782 | 0.855 | 0.828 | 0.8565 |
| table | 0.241 | 0.2235 | 0.241 | 0.241 | 0.287 | 0.279 | 0.3105 |
| dog | 0.7275 | 0.7335 | 0.7275 | 0.7275 | 0.7875 | 0.7535 | 0.791 |
| horse | 0.7725 | 0.7765 | 0.7725 | 0.7725 | 0.8185 | 0.812 | 0.8325 |
| motorbike | 0.2145 | 0.2075 | 0.2145 | 0.2145 | 0.238 | 0.2365 | 0.248 |
| person | 0.415 | 0.3935 | 0.415 | 0.415 | 0.4905 | 0.5155 | 0.5335 |
| plant | 0.4955 | 0.5005 | 0.4955 | 0.4955 | 0.564 | 0.5215 | 0.549 |
| sheep | 0.6585 | 0.6725 | 0.6585 | 0.6585 | 0.7475 | 0.7115 | 0.7495 |
| sofa | 0.453 | 0.445 | 0.453 | 0.453 | 0.5465 | 0.5675 | 0.5775 |
| train | 0.61 | 0.5707 | 0.61 | 0.61 | 0.656 | 0.636 | 0.656 |
| tvmonitor | 0.4685 | 0.461 | 0.4685 | 0.4685 | 0.547 | 0.5535 | 0.5645 |
| ——– | —— | ——— | ——— | ——– | ——— | ——- | ——– |
| mean | 0.4335 | 0.4265 | 0.4335 | 0.4335 | 0.4834 | 0.4737 | 0.4924 |
可以看到,FMGM 在大部分类别上都取得了最高的匹配精度。
总结
在本文中,我们展示了基于两图的 MGM 是基于张量 MGM 的一种特殊情况。基于这一发现,我们提出了一种新的 MGM 方法,不仅降低了复杂性,还避免了循环一致性问题。此外,我们还将亲和矩阵的因子分解引入到我们的工作中,以进一步降低复杂性。为了缓解 MGM 中的局部最大问题,我们还提出了一种基于随机梯度下降方法的近似算法。仿真数据和真实数据实验均证明了我们方法的效率和准确性。然而,由于近似算法中使用的更新策略,当图的数量较大时,FMGM 可能需要更多时间来找到更好的解。此外,当待匹配的图之间存在复杂关系时,FMGM 的性能可能不尽如人意。如何克服 FMGM 的这两个局限性将是我们未来研究的课题。